
科目: 来源: 题型:
【题目】如图,四边形ABCD是⊙O的内接四边形,∠ABC=2∠D,连接OA、OB、OC、AC,OB与AC相交于点E.
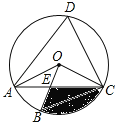
(1)求∠OCA的度数;
(2)若∠COB=3∠AOB,OC=![]() ,求图中阴影部分面积(结果保留π和根号).
,求图中阴影部分面积(结果保留π和根号).
查看答案和解析>>
科目: 来源: 题型:
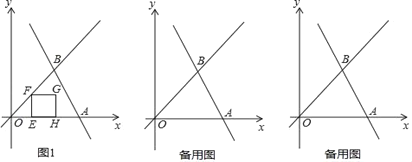
【题目】如图1,直线y=﹣2x+3与x轴交于点A,与直线y=x交于点B.
(1)点A坐标为 ,∠AOB= ;
(2)求S△OAB的值;
(3)动点E从原点O出发,以每秒1个单位长度的速度沿着O→A的路线向终点A匀速运动,过点E作EF⊥x轴交直线y=x于点F,再以EF为边向右作正方形EFGH.设运动t秒时,正方形EFGH与△OAB重叠部分的面积为S.求:S与t之间的函数关系式,并写出t的取值范围.
查看答案和解析>>
科目: 来源: 题型:
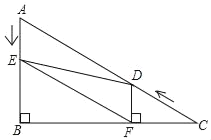
【题目】如图,在Rt△ABC中,∠B=90°,AC=12,∠A=60°.点D从点C出发沿CA方向以每秒2个单位长的速度向A点匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0).过点D作DF⊥BC于点F,连接DE、EF.
(1)AB的长是 .
(2)在D、E的运动过程中,线段EF与AD的关系是否发生变化?若不变化,那么线段EF与AD是何关系,并给予证明;若变化,请说明理由.
(3)四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,AB是半圆O的直径,点C在半圆O上,AB=5cm,AC=4cm.D是弧BC上的一个动点(含端点B,不含端点C),连接AD,过点C作CE⊥AD于E,连接BE,在点D移动的过程中,BE的取值范围是____.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,四边形ABCD中,AD∥BC,AB⊥AC,点E是BC的中点,AE与BD交于点F,且F是AE的中点.
(Ⅰ)求证:四边形AECD是菱形;(Ⅱ)若AC=4,AB=5,求四边形ABCD的面积.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在⊙O中,AB是直径,CD是弦,AB⊥CD,垂足为E,连结CO,AD,∠BAD=20°,则下列说法中正确的是( )

A. ∠BOC=2∠BAD B. CE=EO C. ∠OCE=40° D. AD=2OB
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读资料:小明是一个爱动脑筋的好学生,他在学习了有关圆的切线性质后,意犹未尽,又查阅到了与圆的切线相关的一个问题:
如图1,已知PC是⊙O的切线,AB是⊙O的直径,延长BA交切线PC与P,连接AC、BC、OC.
因为PC是⊙O的切线,AB是⊙O的直径,所以∠OCP=∠ACB=90°,所以∠1=∠2.
又因为∠B=∠1,所以∠B=∠2.
在△PAC与△PCB中,又因为:∠P=∠P,所以△PAC∽△PCB,所以![]() ,即PC2=PAPB.
,即PC2=PAPB.
问题拓展:
(Ⅰ)如果PB不经过⊙O的圆心O(如图2)等式PC2=PAPB,还成立吗?请证明你的结论;
综合应用:
(Ⅱ)如图3,⊙O是△ABC的外接圆,PC是⊙O的切线,C是切点,BA的延长线交PC于点P;
(1)当AB=PA,且PC=12时,求PA的值;
(2)D是BC的中点,PD交AC于点E.求证:![]() .
.

查看答案和解析>>
科目: 来源: 题型:
【题目】某水果生产基地,某天安排30名工人采摘枇杷或草莓(每名工人只能做其中一项工作),并且每人每天摘0.4吨枇杷或0.3吨草莓,当天的枇杷售价每吨2000元,草莓售价每吨3000元,设安排其中x名工人采摘枇杷,两种水果当天全部售出,销售总额达y元.
(1)求y与x之间的函数关系式;
(2)若要求当天采摘枇杷的数量不少于草莓的数量,求销售总额的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com