
科目: 来源: 题型:
【题目】如图,有一个水池,其底面是边长为16尺的正方形,一根芦苇AB生长在它的正中央,高出水面部分BC的长为2尺,如果把该芦苇沿与水池边垂直的方向拉向岸边,那么芦苇的顶部B恰好碰到岸边的B′,则这根芦苇AB的长是( )
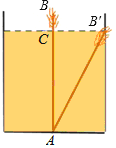
A. 15尺B. 16尺C. 17尺D. 18尺
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l1:![]() 分别与x轴、y轴交于点B、C,且与直线l2:
分别与x轴、y轴交于点B、C,且与直线l2:![]() 交于点A.
交于点A.
(1)求出点A的坐标
(2)若D是线段OA上的点,且△COD的面积为12,求直线CD的解析式
(3)在(2)的条件下,设P是射线CD上的点,在平面内是否存在点Q,使以O、C、P、Q为顶点的四边形是菱形?若存在,直接写出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】为迎接:“国家卫生城市”复检,某市环卫局准备购买A,B两种型号的垃圾箱,通过市场调研得知:购买3个A型垃圾箱和2个B型垃圾箱共需540元,购买2个A型垃圾箱比购买3个B型垃圾箱少用160元.
(1)求每个A型垃圾箱和B型垃圾箱各多少元?
(2)该市现需要购买A,B两种型号的垃圾箱共30个,其中买A型垃圾箱不超过16个.
①求购买垃圾箱的总花费w(元)与A型垃圾箱x(个)之间的函数关系式;
②当买A型垃圾箱多少个时总费用最少,最少费用是多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】将两张完全相同的矩形纸片ABCD、FBED按如图方式放置,BD为重合的对角线.重叠部分为四边形DHBG.

(1)试判断四边形DHBG为何种特殊的四边形,并说明理由;
(2)若AB=8,AD=4,求四边形DHBG的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知函数![]() 与
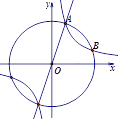
与![]() 的图像在第一象限交于点A(m,y1),点B(m+1,y2)在
的图像在第一象限交于点A(m,y1),点B(m+1,y2)在![]() 的图像上,且点B在以O 点为圆心,OA为半径的⊙O上,则k的值为( ).
的图像上,且点B在以O 点为圆心,OA为半径的⊙O上,则k的值为( ).
A. ![]() B. 1 C.
B. 1 C. ![]() D. 2
D. 2
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知 A、B 两点的坐标分别为(﹣2,0)、(0,1),⊙C 的圆心坐标为(0,﹣1),半径为 1,E 是⊙C 上的一动点,则△ABE 面积的最大值为( )
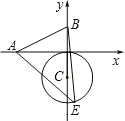
A. ![]() B. 3+
B. 3+![]() C. 3+
C. 3+![]() D. 4+
D. 4+![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,在矩形ABCD中,P为CD边上一点(DP<CP),∠APB=90°.将ΔADP沿AP翻折得到![]() ,PD′的延长线交边AB于点M,过点B作BN‖MP交DC于点N.
,PD′的延长线交边AB于点M,过点B作BN‖MP交DC于点N.
图1
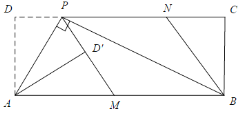
图2
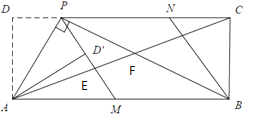
(1)求证:![]() ;
;
(2)请判断四边形PMBN的形状,并说明理由;
(3)如图2,连接AC,分别交PM,PB于点E,F.若tan∠PAD=![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
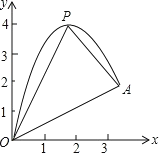
【题目】如图,裕安中学体育训练中,一实心球从斜坡O点处抛出,球的抛出路线可以用二次函数![]() 刻画,斜坡可以用一次函数
刻画,斜坡可以用一次函数![]() 刻画,实心球的落点A的坐标是(
刻画,实心球的落点A的坐标是(![]() ).
).
(1)求二次函数解析式和二次函数图象的最高点P的坐标;
(2)连接抛物线的最高点P与点O、A得△POA,求△POA的面积;
查看答案和解析>>
科目: 来源: 题型:
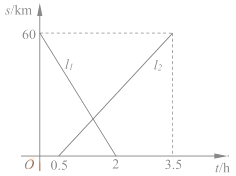
【题目】A、B两地相距60km,甲、乙两人从两地出发相向而行,甲先出发.图中![]() 表示两人离A地的距离S(km)与时间t(h)的关系,结合图像回答下列问题:
表示两人离A地的距离S(km)与时间t(h)的关系,结合图像回答下列问题:
(1)表示乙离开A地的距离与时间关系的图像是________(填![]() );
);
甲的速度是__________km/h;乙的速度是________km/h。
(2)甲出发后多少时间两人恰好相距5km?
查看答案和解析>>
科目: 来源: 题型:
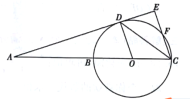
【题目】如图,点D是⊙O上一点,直线AE经过点D,直线AB经过圆心O,交⊙O于B,C两点,CE⊥AE,垂足为点E,交⊙O于点F,∠BCD=∠DCF
(1)求∠A+∠BOD的度数;
(2)若sin∠DCE=![]() ,⊙O的半径为5,求线段AB的长.
,⊙O的半径为5,求线段AB的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com