
科目: 来源: 题型:
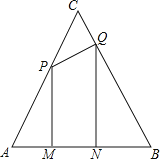
【题目】如图,等边三角形ABC的边长为8cm,动点P从点A出发以![]() 秒的速度沿AC方向向终点C运动,同时动点Q从点C出发以
秒的速度沿AC方向向终点C运动,同时动点Q从点C出发以![]() 秒的速度沿CB方向向终点B运动,过点P、Q分别作边AB的垂线段PM、QN,垂足分别为点M、
秒的速度沿CB方向向终点B运动,过点P、Q分别作边AB的垂线段PM、QN,垂足分别为点M、![]() 设P、Q两点运动时间为t秒
设P、Q两点运动时间为t秒![]() ,四边形MNQP的面积为
,四边形MNQP的面积为![]() .
.
![]() 为何值时,
为何值时,![]() 为等边三角形?
为等边三角形?
![]() 是否存在某一时刻t,使四边形MNQP的面积S等于
是否存在某一时刻t,使四边形MNQP的面积S等于![]() 的面积的
的面积的![]() ?若存在,求出此时t的值;若不存在,说明理由.
?若存在,求出此时t的值;若不存在,说明理由.
![]() 连接PN、QM交于点D,是否存在某一时刻t,使
连接PN、QM交于点D,是否存在某一时刻t,使![]() ?若存在,求出此时t的值;若不存在,说明理由.
?若存在,求出此时t的值;若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
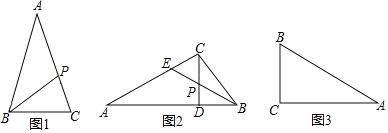
【题目】已知P为![]() 所在平面内一点,连接PA,PB,PC,在
所在平面内一点,连接PA,PB,PC,在![]() ,
,![]() 和
和![]() 中,若存在一个三角形与
中,若存在一个三角形与![]() 相似
相似![]() 全等除外
全等除外![]() 那么就称P为
那么就称P为![]() 的共相似点”根据“共相似点“是否落在三角形的内部,边上或外部,可将其分为内共相似点”,“边共相似点或“外共相似点”.
的共相似点”根据“共相似点“是否落在三角形的内部,边上或外部,可将其分为内共相似点”,“边共相似点或“外共相似点”.
![]() 据定义可知,等边三角形______
据定义可知,等边三角形______![]() 填“存在”或“不存在
填“存在”或“不存在![]() 共相似点
共相似点
(探究)用边共相似点探究三角形的形状
![]() 如图1,若
如图1,若![]() 的一个边共相似点P与其对角项点B的连线,将
的一个边共相似点P与其对角项点B的连线,将![]() 分割成的两个三角形恰与原三角形均相似,试判断
分割成的两个三角形恰与原三角形均相似,试判断![]() 的形状,并说明理由.
的形状,并说明理由.
(探究2)用内共相似点探究三角形的内角关系
![]() 如图2,在
如图2,在![]() 中,
中,![]() ,高线CD与角平分线BE交于点P,若P是
,高线CD与角平分线BE交于点P,若P是![]() 的一个内共相似点试说明点E是
的一个内共相似点试说明点E是![]() 的边共相似点,并直接写出
的边共相似点,并直接写出![]() 的度数;
的度数;
(探究)探究直角三角形共相似点的个数
![]() 如图3,在
如图3,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,若
,若![]() 与
与![]() 相以,则满足条件的P点共有______个
相以,则满足条件的P点共有______个![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】我市某社会团体组织人员参观皇窑瓷展,主办方对团体购票实行优惠:在原定票价的基础上,每张降价40元,则按原定票价需花费6000元购买门票,现在只花了4000元.
![]() 求每张门票原定的票价;
求每张门票原定的票价;
![]() 在展览期间,平均每天可售出个人票2000张,现主办方决定对个人购票也采取优惠措施,发现原定票价每降低2元,平均每天可多售出个人票40张,若要使平均每天的个人票收入达到241500元,且能有效控制游览人数,则票价应降低多少元?
在展览期间,平均每天可售出个人票2000张,现主办方决定对个人购票也采取优惠措施,发现原定票价每降低2元,平均每天可多售出个人票40张,若要使平均每天的个人票收入达到241500元,且能有效控制游览人数,则票价应降低多少元?
查看答案和解析>>
科目: 来源: 题型:
【题目】在课堂上,老师将除颜色外都相同的1个黑球和若干个白球放入一个不透明的口袋并搅匀,让全班同学依次进行摸球试验,每次随机摸出一个球,记下颜色再放回搅匀,下表是试验得到的一组数据.
摸球的次数n | 100 | 150 | 200 | 500 | 800 |
摸到黑球的次数m | 26 | 37 | 49 | 124 | 200 |
摸到黑球的频率 |
|
|
|
| a |
![]() 表中a的值等于______;
表中a的值等于______;
![]() 估算口袋中白球的个数;
估算口袋中白球的个数;
![]() 用画树状图或列表的方法计算连续两名同学都摸出白球的概率.
用画树状图或列表的方法计算连续两名同学都摸出白球的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】某小组做“用频率估计概率”的实验时,统计了某一结果出现的频率,绘制了如图的折线统计图,则符合这一结果的实验最有可能的是![]()
![]()
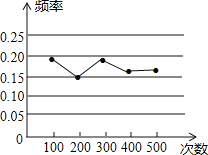
A. 在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”
B. 暗箱中有1个红球和2个黄球,它们只有颜色上的区别,从中任取一球是黄球
C. 掷一个质地均匀的正六面体骰子,向上的面点数是4
D. 掷一枚一元硬币,落地后正面朝上
查看答案和解析>>
科目: 来源: 题型:
【题目】对于给定的两个函数![]() 和
和![]() ,在这里我们把
,在这里我们把![]() 叫做这两个函数的积函数,把直线
叫做这两个函数的积函数,把直线![]() 和
和![]() 叫做抛物线
叫做抛物线![]() 的母线.
的母线.
(1)直接写出函数![]() 和
和![]() 的积函数,然后写出这个积函数的图象与x轴交点的坐标.
的积函数,然后写出这个积函数的图象与x轴交点的坐标.
(2)点P在(1)中的抛物线上,过点P垂直于x轴的直线分别交此抛物线的母线于M、N两点,设点P的横坐标为m,求![]() 时m的值.
时m的值.
(3)已知函数![]() 和
和![]() .当它们的积函数自变量的取值范围是
.当它们的积函数自变量的取值范围是![]() ,且当
,且当![]() 时,这个积函数的最大值是8,求n的值以及这个积函数的最小值.
时,这个积函数的最大值是8,求n的值以及这个积函数的最小值.
查看答案和解析>>
科目: 来源: 题型:
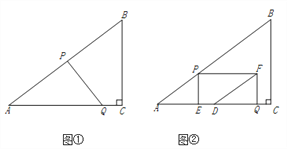
【题目】如图①,在Rt△ABC中,∠C=90°,AB=10,BC=6.点P从点A出发,沿折现AB—BC向终点C运动,在AB上以每秒5个单位长度的速度运动,在BC上以每秒3个单位长度的速度运动.点Q从点C出发,沿CA方向以每秒![]() 个单位长度的速度运动.点P、Q两点同时出发,当点P停止时,点Q也随之停止.设点P运动的时间为t秒.
个单位长度的速度运动.点P、Q两点同时出发,当点P停止时,点Q也随之停止.设点P运动的时间为t秒.
(1)求线段AQ的长.(用含t的代数式表示)
(2)当PQ与△ABC的一边平行时,求t的值
(3)如图②,过点P作PE⊥AC于点E,以PE、QE为邻边作矩形PEQF,点D为AC的中点,连结DF.直接写出DF将矩形PEQF分成两部分的面积比为1:2时t的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】问题情境
小明和小丽共同探究一道数学题:
如图①,在△ABC中,点D是边BC的中点,∠BAD=65°,∠DAC=50°,AD=2,
求AC.
探索发现
小明的思路是:延长AD至点E,使DE=AD,构造全等三角形.
小丽的思路是:过点C作CE∥AB,交AD的延长线于点E,构造全等三角形.
选择小明、小丽其中一人的方法解决问题情境中的问题.
类比应用
如图②,在四边形ABCD中,对角线AC、BD相交于点O,点O是BD的中点,
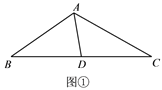

AB⊥AC.若∠CAD=45°,∠ADC=67.5°,AO=2,则BC的长为___________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com