
科目: 来源: 题型:
【题目】如图,在Rt△OAB中,OA=4,AB=5,点C在OA上,AC=1,⊙P的圆心P在线段BC上,且⊙P与边AB,AO都相切.若反比例函数![]() (k≠0)的图象经过圆心P,则k=________________。
(k≠0)的图象经过圆心P,则k=________________。

查看答案和解析>>
科目: 来源: 题型:
【题目】(2017浙江省湖州市)如图,已知∠AOB=30°,在射线OA上取点O1,以O1为圆心的圆与OB相切;在射线O1A上取点O2,以O2为圆心,O2O1为半径的圆与OB相切;在射线O2A上取点O3,以O3为圆心,O3O2为半径的圆与OB相切;…;在射线O9A上取点O10,以O10为圆心,O10O9为半径的圆与OB相切.若⊙O1的半径为1,则⊙O10的半径长是______.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图正方形ABCD的边长为4,点E是AB上的一点,将△BCE沿CE折叠至△FCE,若CF,CE恰好与以正方形ABCD的中心为圆心的⊙O相切,则折痕CE的长为()
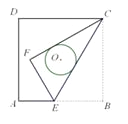
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,正六边形ABCDEF中,P、Q两点分别为△ACF、△CEF的内心.若AF=2,则PQ的长度为何?( )
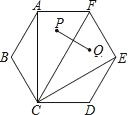
A. 1 B. 2 C. 2![]() ﹣2 D. 4﹣2
﹣2 D. 4﹣2![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】定义:对于给定的一个二次函数,其图象沿x轴翻折后,得到的图象所对应的二次函数称为原二次函数的横翻函数.
(1)直接写出二次函数y=2x2的横翻函数的表达式.
(2)已知二次函数y=x2+bx+c的图象经过点A(﹣3,1)、B(2,6).
①求b、c的值.
②求二次函数y=x2+bx+c的横翻函数的顶点坐标.
③若将二次函数y=x2+bx+c的图象位于A、B两点间的部分(含A、B两点)记为G,则当二次函数y=﹣x2﹣bx﹣c+m与G有且只有一个交点时,直接写出m的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,∠MAN=30°,点C、B分别在射线AM、AN上,AB=6,∠ACB=30°.动点P从点A出发,沿射线AN以每秒3个单位长度的速度运动.过点P作PQ⊥AN交射线AM于点Q,点E是线段AQ的中点,连结PE.设△PQE与△ABC重叠部分图形的面积为S平方单位,点P的运动时间为t秒(t>O).
(1)求PQ的长(用含t的代数式表示).
(2)当点Q在边AC上时,求S与t之间的函数关系式.
(3)当△PQE与△ABC重叠部分图形是一个面积为![]() 的三角形时,求t的值.
的三角形时,求t的值.
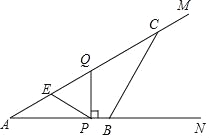
查看答案和解析>>
科目: 来源: 题型:
【题目】探究:如图①,在ABCD中,E为BC的中点,AE与BD相交于点M.求证:![]() .
.
应用:如图②,在四边形ABCD中,AB∥CD,AB=2CD,点E、F分别为AB、BC的中点,EF与BD相交于点M,连结AC.若ME=3,则AC的长为 .
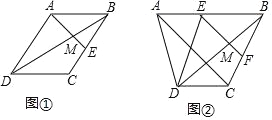
查看答案和解析>>
科目: 来源: 题型:
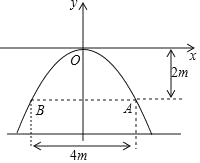
【题目】有一个截面的边缘为抛物线的拱桥桥洞,桥洞壁离水面AB的最大高度是2米,水面宽度AB为4米.把截面图形放在如图所示的平面直角坐标系中.
(1)求这条抛物线对应的函数表达式.
(2)若水面下降1米,求水面宽度增加了多少米?
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系中,抛物线y=ax2+bx经过点A(2,4)和点B(6,0).
(1)求这条抛物线所对应的二次函数的解析式;
(2)直接写出它的开口方向、顶点坐标;
(3)点(x1,y1),(x2,y2)均在此抛物线上,若x1>x2>4,则y1 ________ y2(填“>”“=”或“<”).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com