
科目: 来源: 题型:
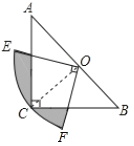
【题目】如图,在△ABC中,∠C=90°,AC=BC,斜边AB=2,O是AB的中点,以O为圆心,线段OC的长为半径画圆心角为90°的扇形OEF,弧EF经过点C,则图中阴影部分的面积为________.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,AB是半径为4的⊙O的直径,P是圆上异于A,B的任意一点,∠APB的平分线交⊙O于点 C,连接AC和BC,△ABC的中位线所在的直线与⊙O相交于点E、F,则EF的长是________

查看答案和解析>>
科目: 来源: 题型:
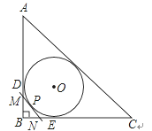
【题目】如图,Rt△ABC的内切圆⊙O与两直角边AB,BC分别相切于点D、E,过劣弧DE(不包括端点D,E)上任一点P作⊙O的切线MN与AB,BC分别交于点M,N,若⊙O的半径为4cm,则Rt△MBN的周长为________cm.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,BC=4,以点A为圆心,2为半径的⊙A与BC相切于点D,交AB于点E,交AC于点F,点P是⊙A上的一点,且∠EPF=45°,则图中阴影部分的面积为( )

A. 4﹣2π B. 8+π C. 4﹣π D. 8﹣2π
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,四边形ABCD的四个顶点分别在反比例函数y=![]() 与y=
与y=![]() (x>0,0<m<n)的图象上,对角线BD∥y轴,且BD⊥AC于点P.已知点B的横坐标为4.
(x>0,0<m<n)的图象上,对角线BD∥y轴,且BD⊥AC于点P.已知点B的横坐标为4.
(1)当m=4,n=20时.
①若点P的纵坐标为2,求直线AB的函数表达式.
②若点P是BD的中点,试判断四边形ABCD的形状,并说明理由.
(2)四边形ABCD能否成为正方形?若能,求此时m,n之间的数量关系;若不能,试说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】问题情境:
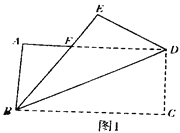
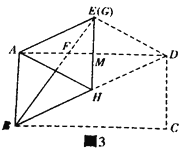
在综合实践课上,张老师让同学们以“矩形的折叠”为主题开展数学活动,张老师拿着一张矩形纸片ABCD,其中AB=acm, AD=bcm, 如图1,先沿对角线BD折叠,点C落在点E的位置,BE交AD于点F.
操作发现:
(1)“奋进”小组发现与BF的长度一定相等的线段是哪一条;
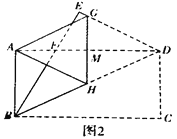
(2)如图2.“雄鹰”小组将图1再折叠一次,使点D与点A重合,得到折痕GH,GH交AD于点M,发现△DGH是等腰三角形,请你证明这个结论;
实践探究:
(3)“创新”小组将自己准备的矩形纸片按照(2)中“雄鹰”小组的作法操作,发现点E和点G重合,,如图3,试探究“创新”小组准备的矩形纸片中a与b满足的数量关系;
(4)”爱心”小组在其他小组的基础上提出问题:当a与b满足什么关系时,点G是DE的中点?请你直接出a与b满足的关系.
查看答案和解析>>
科目: 来源: 题型:
【题目】为了了解高峰时段37路公交车从总站乘该路车出行的人数,随机抽查了10个班次乘该路车人数,结果如下:16,25,18,27,25,30,28,29,25,27.
(1)请求出这10个班次乘该路车人数的平均数、众数与中位数;
(2)如果37路公交车在高峰时段从总站共发出50个班次,根据上面的计算结果,估计在高峰时段从总站乘该路车出行的乘客共有多少人?
查看答案和解析>>
科目: 来源: 题型:
【题目】列方程解应用题:某玩具厂生产一种玩具,按照控制固定成本降价促销的原则,使生产的玩具能够及时售出,据市场调查:每个玩具按480元销售时,每天可销售160个;若销售单价每降低1元,每天可多售出2个。已知每个玩具的固定成本为360元.设每个玩具降价x元,请解决下列问题:
(1)降价后该玩具的日销售量为多少个,每个玩具盈利多少元;(用含x的代数式表示)
(2)若上述条件不变,每个玩具降价多少元时,厂家每天可获利润20000元?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,矩形ABCD的对角线相交于点O,DE∥CA,AE∥BD.
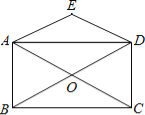
(1)求证:四边形AODE是菱形;
(2)若将题设中“矩形ABCD”这一条件改为“菱形ABCD”,其余条件不变,则四边形AODE的形状是什么?说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com