
科目: 来源: 题型:
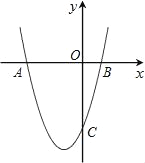
【题目】如图,抛物线y=x2+bx+c经过点A(﹣4,0)和C点(0,﹣4),与x轴另一个交点为B.
(1)求此二次函数的解析式和顶点D的坐标;
(2)求出A、B两点之间的距离;
(3)直接写出当y>﹣4时,x的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知直线y=x+2交x轴、y轴分别于点A、B,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣![]() ,且抛物线经过A、B两点,交x轴于另一点C.
,且抛物线经过A、B两点,交x轴于另一点C.
(1)求抛物线的解析式;
(2)点M是抛物线x轴上方一点,∠MBA=∠CBO,求点M的坐标;
(3)过点A作AB的垂线交y轴于点D,平移直线AD交抛物线于点E、F两点,连结EO、FO.若△EFO为以EF为斜边的直角三角形,求平移后的直线的解析式.

查看答案和解析>>
科目: 来源: 题型:
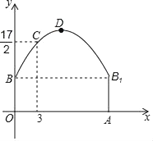
【题目】如图,隧道的截面由抛物线和长方形构成,长方形的长是12m,宽是4m.按照图中所示的直角坐标系,抛物线最高点D到墙面OB的水平距离为6m时,隧道最高点D距离地面10m.
(1)求该抛物线的函数关系式;
(2)一辆货运汽车载一长方体集装箱后宽为4m,高为6m,如果隧道内设双向行车道,那么这辆货车能否安全通过?
(3)在抛物线型拱壁上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度不超过8m,那么两排灯的水平距离最小是多少米?
查看答案和解析>>
科目: 来源: 题型:
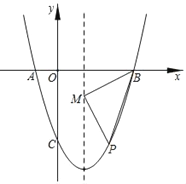
【题目】抛物线的顶点为(1,﹣4),与x轴交于A、B两点,与y轴负半轴交于C(0,﹣3).
(1)求抛物线的解析式;
(2)点P为对称轴右侧抛物线上一点,以BP为斜边作等腰直角三角形,直角顶点M落在对称轴上,求P点的坐标.
查看答案和解析>>
科目: 来源: 题型:
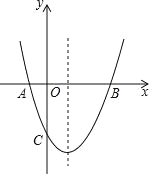
【题目】如图,抛物线y=x2﹣2x﹣3与x轴交于A,B两点(A在B的左侧),顶点为C.
(1)求A,B两点的坐标;
(2)若将该抛物线向上平移t个单位后,它与x轴恰好只有一个交点,求t的值.
查看答案和解析>>
科目: 来源: 题型:
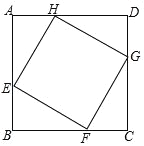
【题目】如图,正方形ABCD的边长为8,E、F、G、H分别是AB、BC、CD、DA上的动点,且AE=BF=CG=DH.
(1)判断四边形EFGH的形状.(直接写结论,不必证明)
(2)设BE=x,四边形EFGH的面积为S,请真接写出S与x的数解析式,并求出S的最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某汽车厂决定把一块长100m、宽60m的矩形空地建成停车场.设计方案如图所示,阴影区域为绿化区(四块绿化区为全等的矩形),空白区域为停车位,且四周的4个出口宽度相同,其宽度不小于28m,不大于52m.设绿化区较长边为xm,停车场的面积为ym2
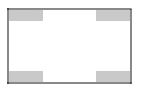
(1)直接写出:
①用x的式子表示出口的宽度为_____.
②y与x的函数关系式及x的取值范围.
(2)求停车场的面积y的最大值.
(3)预计停车场造价为100元/m2,绿化区造价为50元/m2.如果汽车厂投资不得超过540000元建造,当x为整数时,共有几种建造方案?
查看答案和解析>>
科目: 来源: 题型:
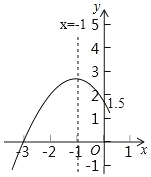
【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图所示.
(1)确定二次函数的解析式;
(2)若方程ax2+bx+c=k有两个不相等的实数根,求k的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】某城市对居民生活用水按以下规定收取每月的水费:家庭月用水量如果不超过8吨,按每吨2.5元收费;如果超过8吨,未超过的部分仍按每吨2.5元收取,而超过部分则按每吨4元收取.
(1)设某家庭月用水量为x吨,水费为y元,请写出y与x之间的函数解析式,并在给定的平面直角坐标系中,画出该函数的图象;
(2)如果小明家按题中规定今年3月份应缴水费34元,那么今年3月份小明家用水多少吨?

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=﹣x+3与抛物线![]() 交于A、B两点,点A在x轴上,点B的横坐标为
交于A、B两点,点A在x轴上,点B的横坐标为![]() .动点P在抛物线上运动(不与点A、B重合),过点P作y轴的平行线,交直线AB于点Q.当PQ不与y轴重合时,以PQ为边作正方形PQMN,使MN与y轴在PQ的同侧,连结PM.设点P的横坐标为m.
.动点P在抛物线上运动(不与点A、B重合),过点P作y轴的平行线,交直线AB于点Q.当PQ不与y轴重合时,以PQ为边作正方形PQMN,使MN与y轴在PQ的同侧,连结PM.设点P的横坐标为m.
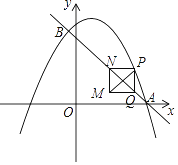
(1)求b、c的值.
(2)当点N落在直线AB上时,直接写出m的取值范围.
(3)当点P在A、B两点之间的抛物线上运动时,设正方形PQMN的周长为C,求C与m之间的函数关系式,并写出C随m增大而增大时m的取值范围.
(4)当△PQM与坐标轴有2个公共点时,直接写出m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com