
科目: 来源: 题型:
【题目】周末,小华和小亮想用所学的数学知识测量家门前小河的宽.测量时,他们选择了河对岸边的一棵大树,将其底部作为点A,在他们所在的岸边选择了点B,使得AB与河岸垂直,并在B点竖起标杆BC,再在AB的延长线上选择点D竖起标杆DE,使得点E与点C、A共线.
已知:CB⊥AD,ED⊥AD,测得BC=1m,DE=1.5m,BD=8.5m.测量示意图如图所示.请根据相关测量信息,求河宽AB.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在正方形ABCD中,E为BC边上一点,连结AE.已知AB=8,CE=2,F是线段AE上一动点.若BF的延长线交正方形ABCD的一边于点G,且满足AE=BG,则![]() 的值为________.
的值为________.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在矩形ABCD中,E是AD边的中点,BE⊥AC于点F,连接DF,分析下列五个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④S四边形CDEF=![]() S△ABF,其中正确的结论有________个。
S△ABF,其中正确的结论有________个。

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在矩形ABCD中,AB=8,AD=6,点M为对角线AC上的一个动点(不与端点A,C重合),过点M作ME⊥AD,MF⊥DC,垂足分别为E,F,则四边形EMFD面积的最大值为( )
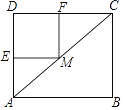
A. 6 B. 12 C. 18 D. 24
查看答案和解析>>
科目: 来源: 题型:
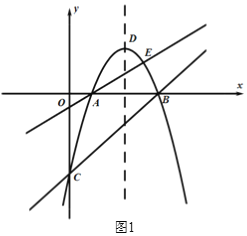
【题目】如图1,抛物线![]() 与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,直线AE:
与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,直线AE:![]() 与抛物线相交于另一点E,点D为抛物线的顶点.
与抛物线相交于另一点E,点D为抛物线的顶点.
(1)求直线BC的解析式及点E的坐标;
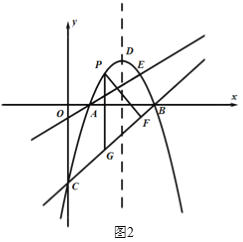
(2)如图2,直线AE上方的抛物线上有一点P,过点P作PF⊥BC于点F,过点P作平行于![]() 轴的直线交直线BC于点G,当△PFG周长最大时,在
轴的直线交直线BC于点G,当△PFG周长最大时,在![]() 轴上找一点M,在AE上找一点N,使得
轴上找一点M,在AE上找一点N,使得![]() 值最小,请求出此时N点的坐标及
值最小,请求出此时N点的坐标及![]() 的最小值;
的最小值;
(3)在第(2)问的条件下,点R为抛物线对称轴上的一点,在平面直角坐标系中是否存在点S,使以点N,E,R,S为顶点的四边形为矩形,若存在,请直接写出点S的坐标,若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读下列材料,并解决问题:任意一个大于1的正整数m都可以表示为:m=p2+q(p、q是正整数),在m的所有这种表示中,如果![]() 最小时,规定:F(m)=
最小时,规定:F(m)=![]() .例如:21可以表示为:21=12+20=22+17=32+12=42+5,因为
.例如:21可以表示为:21=12+20=22+17=32+12=42+5,因为![]() >
>![]() >
>![]() >
>![]() ,所以F(21)=
,所以F(21)=![]() .
.
(1)求F(33)的值;
(2)如果一个正整数n可以表示为t2-t(其中t≥2,且是正整数),那么称n是次完全平方数,证明:任何一个次完全平方数n,都有F(n)=1;
(3)一个三位自然数k,k=100a+10b+c(其中1≤a≤9,0≤b≤9,0≤c≤9,且a≤c,a、b、c为整数),满足十位上的数字恰好等于百位上的数字与个位上的数字之和,且k与其十位上数字的2倍之和能被9整除,求所有满足条件的k中F(k)的最小值.
查看答案和解析>>
科目: 来源: 题型:
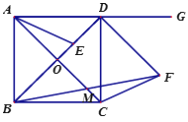
【题目】如图,已知正方形ABCD,对角线AC、BD交于点O,点E在对角线BD上,连接AE.点G是AD延长线上一点,DF平分∠GDC,且DF=BE,连接FB、FC,FB与AC交于点M.
(1)若点E是BD的三等分点(DE<BE),BF=![]() ,求△ABE的面积;
,求△ABE的面积;
(2)求证:DE=2CM.
查看答案和解析>>
科目: 来源: 题型:
【题目】四季水果店正准备促销广西“脆皮桔”和山东烟台“红富士苹果”,已知“脆皮桔”的进价为12元/千克,售价为24元/千克,“红富士苹果”的进价为10元/千克,售价为20元/千克,第一天该店销售两种水果共获利1156元,其中“脆皮桔”的销量比“红富士苹果”销量的4倍少10千克.
(1)求第一天这两种水果的销量分别是多少千克?
(2)该店在第一天的售价基础上销售一段时间后,天气突然变冷不利于“脆皮桔”的保存,为了更好的销售这两种水果,店主决定对“脆皮桔”在原来售价基础上降价a%,销量在原有基础上增加![]() a%,“红富士苹果”在原来售价基础上提升
a%,“红富士苹果”在原来售价基础上提升![]() a%,销量比原来上升了30千克,其中两种水果的进价均不变,结果每天获利比原来多300元,求a的值.
a%,销量比原来上升了30千克,其中两种水果的进价均不变,结果每天获利比原来多300元,求a的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知直线y=-x+3与x轴、y轴分别交于A,B两点,抛物线y=-x2+bx+c经过B点,且与x轴交于C,D两点(点C在左侧),且C(-3,0).
(1)求抛物线的解析式;
(2)平移直线AB,使得平移后的直线与抛物线分别交于点D,E,与y轴交于点F,连接CE,CF,求△CEF的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com