
科目: 来源: 题型:
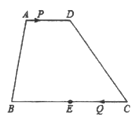
【题目】如图,在四边形![]() 中,
中,![]() ,
, ![]() 是
是![]() 的中点.点
的中点.点![]() 以每秒1个单位长度的速度从点
以每秒1个单位长度的速度从点![]() 出发,沿
出发,沿![]() 向点
向点![]() 运动;点
运动;点![]() 同时以每秒3个单位长度的速度从 点
同时以每秒3个单位长度的速度从 点![]() 出发,沿
出发,沿![]() 向点
向点![]() 运动.点
运动.点![]() 停止运动时,点
停止运动时,点![]() 也随之停止运动.当运动时间
也随之停止运动.当运动时间![]() 秒时,以点
秒时,以点![]() 为顶点的四边形是平行四边形.则
为顶点的四边形是平行四边形.则![]() 的值为_________.
的值为_________.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知二次函数的解析式是y=x2﹣2x﹣3.
(1)与y轴的交点坐标是 ,顶点坐标是 .
(2)在坐标系中利用描点法画出此抛物线;
x | … | … | |||||
y | … | … |
(3)结合图象回答:当﹣2<x<2时,函数值y的取值范围是 .
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系xOy中,对于P,Q两点给出如下定义:若点P到两坐标轴的距离之和等于点Q到两坐标轴的距离之和,则称P,Q两点为同族点.下图中的P,Q两点即为同族点.
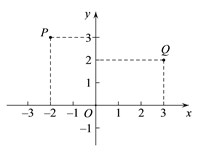
(1)已知点A的坐标为(![]() ,1),
,1),
①在点R(0,4),S(2,2),T(2, ![]() )中,为点A的同族点的是 ;
)中,为点A的同族点的是 ;
②若点B在x轴上,且A,B两点为同族点,则点B的坐标为 ;
(2)直线l: ![]() ,与x轴交于点C,与y轴交于点D,
,与x轴交于点C,与y轴交于点D,
①M为线段CD上一点,若在直线![]() 上存在点N,使得M,N两点为同族点,求n的取值范围;
上存在点N,使得M,N两点为同族点,求n的取值范围;
②M为直线l上的一个动点,若以(m,0)为圆心, ![]() 为半径的圆上存在点N,使得M,N两点为同族点,直接写出m的取值范围.
为半径的圆上存在点N,使得M,N两点为同族点,直接写出m的取值范围.
查看答案和解析>>
科目: 来源: 题型:
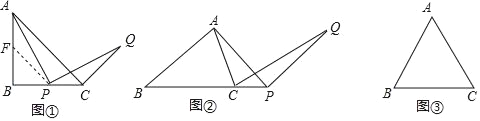
【题目】在△ABC中,BA=BC,∠ABC=α(0°<α<180°),点P为直线BC上一动点(不与点B,C重合),连接AP,将线段PA绕点P顺时针旋转α度得到线段PQ,连接CQ.
(1)当α=90°,且点P在线段BC上时,过P作PF∥AC交直线AB于点F,如图1,图中与△APF全等的是哪个三角形,∠ACQ的度数.
(2)当点P在BC延长线上,AB:AC=m:n时,如图2,试求线段BP与CQ的比值;
(3)当点P在直线BC上,α=60°,∠APB=30°,CP=4时,请直接写出线段CQ的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线C1:y=mx2﹣2mx+m+4与y轴交于点A(0,3),与x轴交于点B、C(点B在点C左侧).
(1)求该抛物线的解析式;
(2)求点B的坐标;
(3)若抛物线C2:y=a(x﹣1)2﹣1(a≠0)与线段AB恰有一个公共点,结合函数的图象,求a的取值范围.
查看答案和解析>>
科目: 来源: 题型:
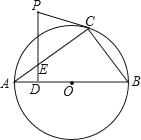
【题目】如图,△ABC内接于⊙O,AB是⊙O的直径.PC是⊙O的切线,C为切点,PD⊥AB于点D,交AC于点E.
(1)求证:∠PCE=∠PEC;
(2)若AB=10,ED=![]() ,sinA=
,sinA=![]() ,求PC的长.
,求PC的长.
查看答案和解析>>
科目: 来源: 题型:
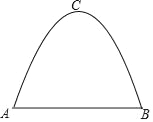
【题目】一条单车道的抛物线形隧道如图所示.隧道中公路的宽度AB=8m,隧道的最高点C到公路的距离为6m.
(1)建立适当的平面直角坐标系,求抛物线的表达式;
(2)现有一辆货车的高度是4.4m,货车的宽度是2m,为了保证安全,车顶距离隧道顶部至少0.5m,通过计算说明这辆货车能否安全通过这条隧道.
查看答案和解析>>
科目: 来源: 题型:
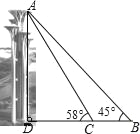
【题目】奥林匹克公园观光塔由五座高度不等、错落有致的独立塔组成.在综合实践活动课中,某小组的同学决定利用测角仪测量这五座塔中最高塔的高度(测角仪高度忽略不计).他们的操作方法如下:如图,他们先在B处测得最高塔塔顶A的仰角为45°,然后向最高塔的塔基直行90米到达C处,再次测得最高塔塔顶A的仰角为58°.请帮助他们计算出最高塔的高度AD约为多少米.(参考数据:sin58°≈0.85,cos58°≈0.53,tan58°≈1.60)
查看答案和解析>>
科目: 来源: 题型:
【题目】在我国古代数学著作《九章算术》中记载了这样一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”用现代语言表述为:如图,AB为⊙O的直径,弦CD⊥AB于点E,AE = 1寸,CD = 10寸,求直径AB的长.请你解答这个问题.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com