
科目: 来源: 题型:
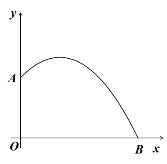
【题目】某广场有一个小型喷泉,水流从垂直于地面的水管OA喷出,OA长为1.5米.水流在各个方向上沿形状相同的抛物线路径落到地面上,某方向上抛物线路径的形状如图所示,落点B到O的距离为3米.建立平面直角坐标系,水流喷出的高度y(米)与水平距离x(米)之间近似满足函数关系![]()
(1)求y与x之间的函数关系式;
(2)求水流喷出的最大高度.

查看答案和解析>>
科目: 来源: 题型:
【题目】京剧脸谱是京剧艺术独特的表现形式.京剧表演中,经常用脸谱象征人物的性格,品质,甚至角色和命运.如红脸代表忠心耿直,黑脸代表强悍勇猛.现有三张不透明的卡片,其中两张卡片的正面图案为“红脸”,另外一张卡片的正面图案为“黑脸”,卡片除正面图案不同外,其余均相同,将这三张卡片背面向上洗匀,从中随机抽取一张,记录图案后放回,重新洗匀后再从中随机抽取一张.
请用画树状图或列表的方法,求抽出的两张卡片上的图案都是“红脸”的概率.(图案为“红脸”的两张卡片分别记为A1、A2,图案为“黑脸”的卡片记为B)

查看答案和解析>>
科目: 来源: 题型:
【题目】下面是小明设计的“作平行四边形的高”的尺规作图过程
已知:平行四边形ABCD.
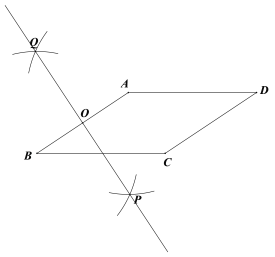
求作:![]() ,垂足为点E.
,垂足为点E.
作法:如图,
①分别以点A和点B为圆心,大于![]() 的长为半径作弧,两弧相交于P,Q两点;
的长为半径作弧,两弧相交于P,Q两点;
②作直线PQ,交AB于点O;
③以点O为圆心,OA长为半径做圆,交线段BC于点E;
④连接AE.
所以线段AE就是所求作的高.
根据小明设计的尺规作图过程
⑴使用直尺和圆规,补全图形;(保留作图痕迹)
⑵完成下面的证明
证明:![]() AP=BP, AQ= ,
AP=BP, AQ= ,
![]() PQ为线段AB的垂直平分线.
PQ为线段AB的垂直平分线.
![]() O为AB中点.
O为AB中点.
![]() AB为直径,⊙O与线段BC交于点E,
AB为直径,⊙O与线段BC交于点E,
![]()
![]()
![]() .( )(填推理的依据)
.( )(填推理的依据)
![]()
![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】下表显示的是某种大豆在相同条件下的发芽试验结果:
每批粒数n | 100 | 300 | 400 | 600 | 1000 | 2000 | 3000 |
发芽的粒数m | 96 | 282 | 382 | 570 | 948 | 1904 | 2850 |
发芽的频率 | 0.960 | 0.940 | 0.955 | 0.950 | 0.948 | 0.952 | 0.950 |
下面有三个推断:
①当n为400时,发芽的大豆粒数为382,发芽的频率为0.955,所以大豆发芽的概率是0.955;
②随着试验时大豆的粒数的增加,大豆发芽的频率总在0.95附近摆动,显示出一定的稳定性,可以估计大豆发芽的概率是0.95;
③若大豆粒数n为4000,估计大豆发芽的粒数大约为3800粒.
其中推断合理的是( )
A. ①②③ B. ①② C. ①③ D. ②③
查看答案和解析>>
科目: 来源: 题型:
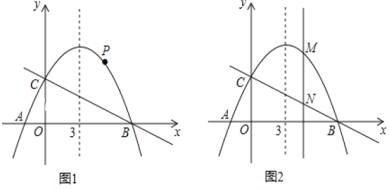
【题目】如图, 已知抛物线![]() 的对称轴是直线x=3,且与x轴相交于A,B两点(B点在A点右侧)与y轴交于C点 .
的对称轴是直线x=3,且与x轴相交于A,B两点(B点在A点右侧)与y轴交于C点 .
(1)求抛物线的解析式和A、B两点的坐标;
(2)若点P是抛物线上B、C两点之间的一个动点(不与B、C重合),则是否存在一点P,使△PBC的面积最大.若存在,请求出△PBC的最大面积;若不存在,试说明理由;
(3)若M是抛物线上任意一点,过点M作y轴的平行线,交直线BC于点N,当MN=3时,求M点的坐标 .
查看答案和解析>>
科目: 来源: 题型:
【题目】已知关于x的方程x2-2(k-1)x+k2 =0有两个实数根x1.x2.
(1)求实 数k的取值范围;
(2)若(x1+1)(x2+1)=2,试求k的值.
查看答案和解析>>
科目: 来源: 题型:
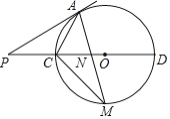
【题目】如图,过⊙O外一点P作⊙O的切线PA切⊙O于点A,连接PO并延长,与⊙O交于C、D两点,M是半圆CD的中点,连接AM交CD于点N,连接AC、CM.
(1)求证:CM2=MN.MA;
(2)若∠P=30°,PC=2,求CM的长.
查看答案和解析>>
科目: 来源: 题型:
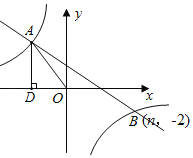
【题目】如图所示,在平面直角坐标系中,一次函数y=kx+b(k≠0)与反比例函数y=![]() (m≠0)的图象交于第二、四象限A、B两点,过点A作AD⊥x轴于D,AD=4,sin∠AOD=
(m≠0)的图象交于第二、四象限A、B两点,过点A作AD⊥x轴于D,AD=4,sin∠AOD=![]() ,且点B的坐标为(n,-2).
,且点B的坐标为(n,-2).
(1)求一次函数与反比例函数的解析式;
(2)E是y轴上一点,且△AOE是等腰三角形,请直接写出所有符合条件的E点坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知抛物线y=ax2-4x+c(a≠0)与反比例函数y=![]() 的图象相交于B点,且B点的横坐标为3,抛物线与y轴交于点C(0,6),A是抛物线y=ax2-4x+c的顶点,P点是x轴上一动点,当PA+PB最小时,P点的坐标为_______.
的图象相交于B点,且B点的横坐标为3,抛物线与y轴交于点C(0,6),A是抛物线y=ax2-4x+c的顶点,P点是x轴上一动点,当PA+PB最小时,P点的坐标为_______.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com