
科目: 来源: 题型:
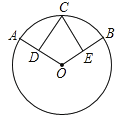
【题目】如图,D、E分别是⊙O两条半径OA、OB的中点,![]() .
.
(1)求证:CD=CE.
(2)若∠AOB=120°,OA=x,四边形ODCE的面积为y,求y与x的函数关系式.
查看答案和解析>>
科目: 来源: 题型:
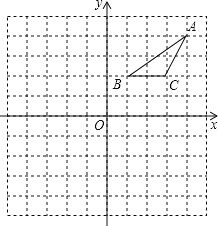
【题目】在正方形网格中建立如图所示的平面直角坐标系xOy.△ABC的三个顶点都在格点上,点A、B、C的坐标分别是A(4,4)、B(1,2)、C(3,2),请解答下列问题.
(1)将△ABC向下平移5个单位长度,画出平移后的△A1B1C1;
(2)画出△A1B1C1关于y轴对称的△A2B2C2;
(3)将△ABC绕点O逆时针旋转90°,画出旋转后的△A3B3C3.并写出点A3的坐标.
查看答案和解析>>
科目: 来源: 题型:
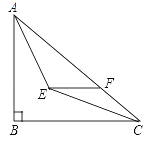
【题目】如图,在Rt△ABC中,∠ABC=90°,AB=6,BC=8,∠BAC与∠ACB的平分线相较于点E,过点E作EF∥BC交AC于点F,则EF的长为________.
查看答案和解析>>
科目: 来源: 题型:
【题目】在甲、乙两个不透明的布袋,甲袋中装有3个完全相同的小球,分别标有数字0,1,2;乙袋中装有3个完全相同的小球,分别标有数字﹣1,﹣2,0;现从甲袋中随机抽取一个小球,记录标有的数字为x,再从乙袋中随机抽取一个小球,记录标有的数字为y,确定点M坐标为(x,y).
(1)用树状图或列表法列举点M所有可能的坐标;
(2)求点M(x,y)在函数y=-x+1的图象上的概率;
(3)在平面直角坐标系xOy中,⊙O的半径是2,求过点M(x,y)能作⊙O的切线的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,已知抛物线![]() 的图像经过点A(1,0),B(0,5),
的图像经过点A(1,0),B(0,5),

(1)求这个抛物线的解析式;
(2)设(1)中的抛物线与x轴的另一个交点为C,求出点C的坐标;并确定在抛物线上是否存在一点E,使△BCE是以BC为斜边的直角三角形?若存在,在图中做出所有的点E(不写画法,保留作图痕迹);若不存在,说明理由;
(3)点P是直线BC上的一个动点(P点不与B点和C点重合),过点P做x轴的垂线,交抛物线于点M,点Q在直线BC上,距离点P为![]() 个单位长度,设点P的横坐标为t,△PMQ的面积为S,求出S与t之间的函数关系式。
个单位长度,设点P的横坐标为t,△PMQ的面积为S,求出S与t之间的函数关系式。
查看答案和解析>>
科目: 来源: 题型:
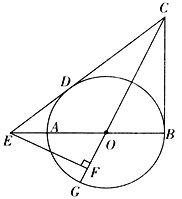
【题目】如图,AB为⊙O的直径,CB,CD分别切⊙O于点B,D,CD交BA的延长线于点E,CO的延长线交⊙O于点G,EF⊥OG于点F。
(1)求证:∠FEB=∠ECF
(2)BC= 12, DE=8 求 EA的长。
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知△ABC内接于⊙O中,AB=![]() ,∠C=60°.
,∠C=60°.
(1)求⊙O的半径;
(2) 若∠CAB=45°,点P从C点出发,沿 弧 CA 向点A滑动,滑动多长距离时△PAB会是等边三角形?
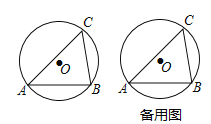
查看答案和解析>>
科目: 来源: 题型:
【题目】九年(1)班的体育课上,小明、小强和小华三人在学习训练足球,足球从一人传到另一人就记为踢一次.
(1)如果从小强开始踢,经过两次踢球后,足球踢到了小明处的概率是多少?请用数状图或列表法说明.
(2)如果踢三次,球踢到了小明处的可能性最小,应从谁开始踢?(直接写出结论)
查看答案和解析>>
科目: 来源: 题型:
【题目】(9分)九年级数学兴趣小组经过市场调查,得到某种运动服每月的销量与售价的相关信息如下表:
售价(元/件) | 100 | 110 | 120 | 130 | … |
月销量(件) | 200 | 180 | 160 | 140 | … |
已知该运动服的进价为每件60元,设售价为![]() 元.
元.
(1)请用含x的式子表示:①销售该运动服每件的利润是 元;②月销量是 件;(直接写出结果)
(2)设销售该运动服的月利润为![]() 元,那么售价为多少时,当月的利润最大,最大利润是多少?
元,那么售价为多少时,当月的利润最大,最大利润是多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,AB是⊙O的直径,C、D是⊙O上的点,且OC∥BD, AD分别与BC,OC相交于点E,F,则下列结论:①AD⊥BD; ②∠AOC=∠AEC; ③CB平分∠ABD;④AF=DF; ⑤BD=2OF; ⑥△CEF ≌△BED,其中一定成立的是( )
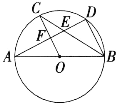
A. ① ③ ⑤ ⑥ B. ① ③ ④ ⑤
C. ② ④ ⑤ ⑥ D. ② ③ ④ ⑥
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com