
科目: 来源: 题型:
【题目】在平面直角坐标系中,直线y=﹣![]() x+a(a>0)分别与x 轴、y 轴交于A、B 两点,C、D 的坐标分别为 C(0,b)、D(2a,b﹣a)(b>a).
x+a(a>0)分别与x 轴、y 轴交于A、B 两点,C、D 的坐标分别为 C(0,b)、D(2a,b﹣a)(b>a).
(1)试判断四边形ABCD的形状,并说明理由;
(2)若点C、D关于直线AB的对称点分别为C′、D′.
①当b=3时,试问:是否存在满足条件的a,使得△BC′D′面积为![]() ?
?
②当点C′恰好落在x轴上时,试求a 与b的函数表达式.
查看答案和解析>>
科目: 来源: 题型:
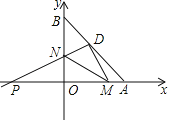
【题目】在平面直角坐标系中,点A和点B分别在x轴的正半轴和y轴的正半轴上,且OA=6,OB=8,点D是AB的中点.
(1)直接写出点D的坐标及AB的长;
(2)若直角∠NDM绕点D旋转,射线DP分别交x轴、y轴于点P、N,射线DM交x轴于点M,连接MN.
①当点P和点N分别在x轴的负半轴和y轴的正半轴时,若△PDM∽△MON,求点N的坐标;
②在直角∠NDM绕点D旋转的过程中,∠DMN的大小是否会发生变化?请说明理由.
查看答案和解析>>
科目: 来源: 题型:
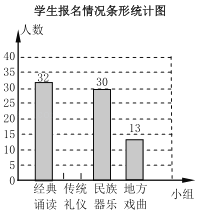
【题目】为推进“传统文化进校园”活动,某校准备成立“经典诵读”、“传统礼仪”、“民族器乐”和“地方戏曲”等四个课外活动小组.学生报名情况如图(每人只能选择一个小组):
(1)报名参加“民族器乐”课外活动小组的学生数占所有报名人数的30%,报名参加课外活动小组的学生共有______人,并将条形统计图补充完整;
(2)根据报名情况,学校决定从报名“地方戏曲”小组的甲、乙、丙三人中随机调整两人到“经典诵读”小组,甲、乙恰好都被调整到“经典诵读”小组的概率是多少?请用列表或画树状图的方法说明.
查看答案和解析>>
科目: 来源: 题型:
【题目】某商店以每件25元的价格购进一批商品,该商品可以自行定价,若每件商品售价a元,则可卖出(400﹣10a)件,但物价局限定每件商品的利润不得超过进价的30%,商店计划要盈利500元,每件商品应定价多少元?需要进货多少件?
查看答案和解析>>
科目: 来源: 题型:
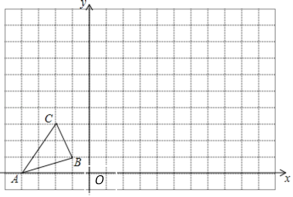
【题目】如图,在 11×16 的网格图中,△ABC 三个顶点坐标分别为 A(﹣4,0),B(﹣1,1),C(﹣2,3).
(1)请画出△ABC 沿x 轴正方向平移4个单位长度所得到的△A1B1C1;
(2)以原点O为位似中心,将(1)中的△A1B1C1 放大为原来的3倍得到△A2B2C2,请在第一象限内画出△A2B2C2,并直接写出△A2B2C2 三个顶点的坐标.
查看答案和解析>>
科目: 来源: 题型:
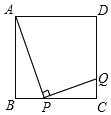
【题目】如图,在正方形ABCD中,AB=4,点P、Q分别在直线CB与射线DC上(点P不与点C、点B重合),且保持∠APQ=90°,CQ=1,则线段BP的长为_____.
查看答案和解析>>
科目: 来源: 题型:
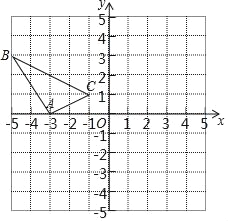
【题目】在边长为1个单位长度的小正方形组成的网格中,建立如图所示的平面直角坐标系△ABC是格点三角形(顶点在网格线的交点上)
(1)先作△ABC关于原点O成中心对称的△A1B1C1,再把△A1B1C1向上平移4个单位长度得到△A2B2C2;
(2)△A2B2C2与△ABC是否关于某点成中心对称?若是,直接写出对称中心的坐标;若不是,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
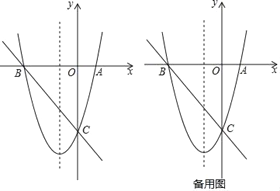
【题目】如图,已知抛物线y=![]() x2+3x﹣8的图象与x轴交于A,B两点(点A在点B的右侧),与y轴交于点C.
x2+3x﹣8的图象与x轴交于A,B两点(点A在点B的右侧),与y轴交于点C.
(1)求直线BC的解析式;
(2)点F是直线BC下方抛物线上的一点,当△BCF的面积最大时,在抛物线的对称轴上找一点P,使得△BFP的周长最小,请求出点F的坐标和点P的坐标;
(3)在(2)的条件下,是否存在这样的点Q(0,m),使得△BFQ为等腰三角形?如果有,请直接写出点Q的坐标;如果没有,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
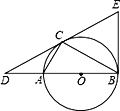
【题目】已知△ABC内接于以AB为直径的⊙O,过点C作⊙O的切线交BA的延长线于点D,且DA∶AB=1∶2.
(1)求∠CDB的度数;
(2)在切线DC上截取CE=CD,连接EB,判断直线EB与⊙O的位置关系,并证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com