
科目: 来源: 题型:
【题目】某学校是乒乓球体育传统项目学校,为进一步推动该项目的开展,学校准备到体育用品店购买直拍球拍和横拍球拍若干副,并且每买一副球拍必须要买10个乒乓球,乒乓球的单价为2元/个,若购买20副直拍球拍和15副横拍球拍花费9000元;购买10副横拍球拍比购买5副直拍球拍多花费1600元.
(1)求两种球拍每副各多少元?
(2)若学校购买两种球拍共40副,且直拍球拍的数量不多于横拍球拍数量的3倍,请你给出一种费用最少的方案,并求出该方案所需费用.
查看答案和解析>>
科目: 来源: 题型:
【题目】某市为提倡节约用水,准备实行自来水“阶梯计费”方式,用户用水不超出基本用水量的部分享受基本价格,超出基本用水量的部分实行加价收费,为更好地做决策,自来水公司随机抽取部分用户的用水量数据,并绘制了如图不完整的统计图(每组数据包括最大值但不包括最小值),请你根据统计图解决下列问题:
(1)此次抽样调查的样本容量是
(2)补全左侧统计图,并求扇形统计图中“25吨~30吨”部分的圆心角度数.
(3)如果自来水公司将基本用水量定为每户25吨,那么该地区6万用户中约有多少用户的用水全部享受基本价格?

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆相交于点D,连接BD、BE、CE,若∠CBD=32°,则∠BEC的度数为________.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90,AC=BC=1,E、F为线段AB上两动点,且∠ECF=45°,过点E、F分别作BC、AC的垂线相交于点M,垂足分别为H、G.现有以下结论:①AB=![]() ;②当点E与点B重合时,MH=
;②当点E与点B重合时,MH=![]() ;③AF+BE=EF;④MGMH=
;③AF+BE=EF;④MGMH=![]() ,其中正确结论的个数是( )
,其中正确结论的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目: 来源: 题型:
【题目】点A为双曲线![]() (x>0)上一点,B为x轴正半轴上一点,线段AB的中点C恰好在双曲线上,则△OAC的面积为( )
(x>0)上一点,B为x轴正半轴上一点,线段AB的中点C恰好在双曲线上,则△OAC的面积为( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目: 来源: 题型:
【题目】已知菱形OABC在平面直角坐标系的位置如图所示,顶点A(5,0),OB=4![]() ,点P是对角线OB上的一个动点,D(0,1),当CP+DP最短时,点P的坐标为( )
,点P是对角线OB上的一个动点,D(0,1),当CP+DP最短时,点P的坐标为( )

A. (0,0) B. (1,![]() ) C. (
) C. (![]() ,
,![]() ) D. (
) D. (![]() ,
,![]() )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,中线BE,CD相交于点O,连接DE,下列结论: ①![]() =
=![]() ; ②
; ②![]() =
=![]() ;③
;③![]() =
=![]() ;④
;④![]() =
=![]() .其中正确的个数有( )
.其中正确的个数有( )
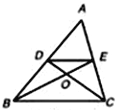
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目: 来源: 题型:
【题目】某班七个兴趣小组人数分别为4,4,5,5,x,6,7,已知这组数据的平均数是5,则这组数据的众数和中位数分别是( )
A. 4,5 B. 4,4 C. 5,4 D. 5,5
查看答案和解析>>
科目: 来源: 题型:
【题目】(问题提出)
“不以规矩,不能成方圆.”——孟子;“圆,一中同长也.”——墨经.
(1)圆,一中同长也.”体现了古代先哲对“圆”定义的思考,请用现代文翻译:____.
(初步思考)
圆规是我们初中几何学习不可或缺的工具,用圆规不仅可以画圆、画弧,还可以画弧与弧的交点,利用这一特征可以构造很多图形,如:
(2)角平分线:如图1,只用圆规在∠AOB中画出一点P使得点P在∠AOB的角平分线上;对称点:如图2,只用圆规画出点P关于直线l的对称点Q,并说明理由.
 (操作与应用)
(操作与应用)
(3)已知点A、直线l.在图3中只用圆规在直线l上画出两点B、C,使得A、B、C恰好是等腰三角形的3个顶点,(画出一个并写出相等线段即可):
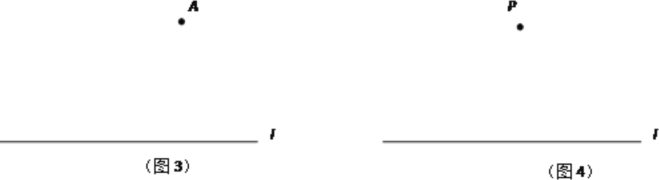
已知点P、直线l.在图4中只用圆规画出一点Q,使得点P、Q所在的直线与直线l平行.(提示:平行四边形对边平行).
(4)已知点O、A、B,只用圆规画出半径为AB的⊙O与点A、B所在直线的交点C、D.

查看答案和解析>>
科目: 来源: 题型:
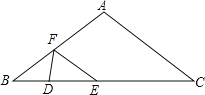
【题目】如图,在△ABC中,AB=AC=10cm,BC=16cm,DE=4cm,线段DE(端点D从点B开始)沿BC边以1cm/s的速度向点C运动,当端点E到达点C时停止运动,过点E作EF∥AC交AB于点F,连接DF,设运动的时间为t秒(t≥0).
(1)用含t的代数式表示线段EF的长度为 ;
(2)在运动过程中,△DEF能否为等腰三角形?若能,请求出t的值;若不能,试说明理由;
(3)若点M是线段EF的中点,请直接写出在整个运动过程中点M运动路线的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com