
科目: 来源: 题型:
【题目】(10分)某工厂计划在规定时间内生产24000个零件,若每天比原计划多生产30个零件,则在规定时间内可以多生产300个零件.
(1)求原计划每天生产的零件个数和规定的天数.
(2)为了提前完成生产任务,工厂在安排原有工人按原计划正常生产的同时,引进5组机器人生产流水线共同参与零件生产,已知每组机器人生产流水线每天生产零件的个数比20个工人原计划每天生产的零件总数还多20%,按此测算,恰好提前两天完成24000个零件的生产任务,求原计划安排的工人人数.
查看答案和解析>>
科目: 来源: 题型:
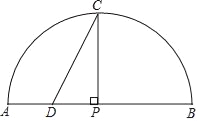
【题目】如图,P是弧AB所对弦AB上一动点,过点P作PC⊥AB交弧AB于点C,取AP中点D,连接CD.已知AB=6cm,设A,P两点间的距离为xcm,C.D两点间的距离为ycm.(当点P与点A重合时,y的值为0;当点P与点B重合时,y的值为3)
小凡根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.
下面是小凡的探究过程,请补充完整:
(1)通过取点、画图、测量,得到了x与y的几组值,如下表:
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y/cm | 0 | 2.2 | 3.2 | 3.4 | 3.3 | 3 |
(2)建立平面直角坐标系,描出补全后的表中各对对应值为坐标的点,画出该函数的图象;
(3)结合所画出的函数图象,解决问题:当∠C=30°时,AP的长度约为多少cm.
查看答案和解析>>
科目: 来源: 题型:
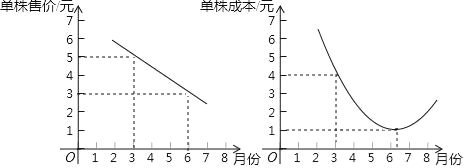
【题目】小哲的姑妈经营一家花店,随着越来越多的人喜爱“多肉植物”,姑妈也打算销售“多肉植物”.小哲帮助姑妈针对某种“多肉植物”做了市场调查后,绘制了以下两张图表:
(1)如果在三月份出售这种植物,单株获利多少元;
(2)请你运用所学知识,帮助姑妈求出在哪个月销售这种多肉植物,单株获利最大?(提示:单株获利=单株售价﹣单株成本)
查看答案和解析>>
科目: 来源: 题型:
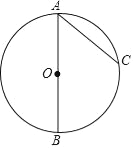
【题目】如图,AB是⊙O的直径,C是⊙O上一点,连接AC.过点B作⊙O的切线,交AC的延长线于点D,在AD上取一点E,使AE=AB,连接BE,交⊙O于点F.
请补全图形并解决下面的问题:
(1)求证:∠BAE=2∠EBD;
(2)如果AB=5,sin∠EBD=![]() .求BD的长.
.求BD的长.
查看答案和解析>>
科目: 来源: 题型:
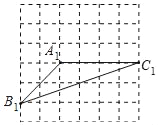
【题目】如图是边长为1的正方形网格,△A1B1C1的顶点均在格点上.
(1)在该网格中画出△A2B2C2(顶点均在格点上),使△A2B2C2∽△A1B1C1;
(2)请写出(1)中作图的主要步骤,并说明△A2B2C2和△A1B1C1相似的依据.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,某学校开展“交通安全日”活动.在活动中,交警叔叔向同学们展示了大货车盲区的分布情况,并提醒大家:坐在驾驶室的司机根本看不到在盲区中的同学们,所以一定要远离大货车的盲区,保护自身安全.小刚所在的学习小组为了更好的分析大货车盲区的问题,将图1用平面图形进行表示,并标注了测量出的数据,如图2.在图2中大货车的形状为矩形,而盲区1为梯形,盲区2、盲区3为直角三角形,盲区4为正方形.
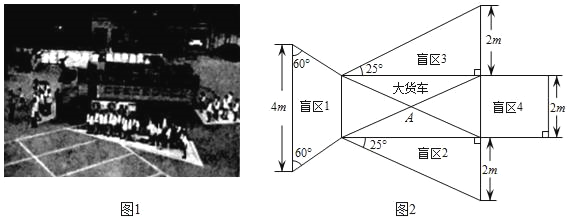
请你帮助小刚的学习小组解决下面的问题:
(1)盲区1的面积约是多少m2;盲区2的面积约是多少m2;
(![]() ≈1.4,
≈1.4,![]() ≈1.7,sin25°≈0.4,cos25°≈0.9,tan25°≈05,结果保留整数)
≈1.7,sin25°≈0.4,cos25°≈0.9,tan25°≈05,结果保留整数)
(2)如果以大货车的中心A点为圆心,覆盖所有盲区的半径最小的圆为大货车的危险区域,请在图2中画出大货车的危险区域.
查看答案和解析>>
科目: 来源: 题型:
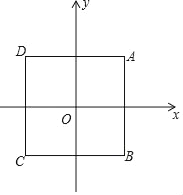
【题目】如图,在平面直角坐标系xOy中,点O为正方形ABCD对角线的交点,且正方形ABCD的边均与某条坐标轴平行或垂直,AB=4.
(1)如果反比例函数y=![]() 的图象经过点A,求这个反比例函数的表达式;
的图象经过点A,求这个反比例函数的表达式;
(2)如果反比例函数y=![]() 的图象与正方形ABCD有公共点,请直接写出k的取值范围.
的图象与正方形ABCD有公共点,请直接写出k的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】函数y=mx2﹣2mx﹣3m是二次函数.
(1)如果该二次函数的图象与y轴的交点为(0,3),求m的值;
(2)在给定的坐标系中画出(1)中二次函数的图象.
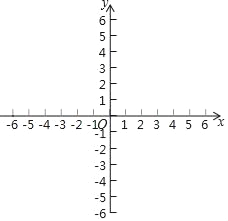
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读下面材料:
在数学课上,老师请同学们思考如下问题:
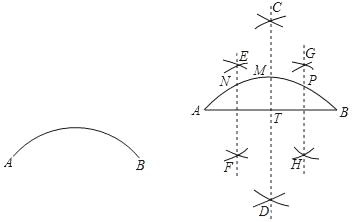
请利用直尺和圆规四等分弧AB.
小亮的作法如下:
如图,
(1)连接AB;
(2)作AB的垂直平分线CD交弧AB于点M.交AB于点T;
(3)分别作线段AT,线段BT的垂直平分线EF,GH,交弧AB于N,P两点;
那么N,M,P三点把弧AB四等分.
老师问:“小亮的作法正确吗?”
请回备:小亮的作法_____(“正确”或“不正确”)理由是_____.
查看答案和解析>>
科目: 来源: 题型:
【题目】刘徵是我国古代最杰出的数学家之一,他在《九算术圆田术)中用“割圆术”证明了圆面积的精确公式,并给出了计算圆周率的科学方法(注:圆周率=圆的周长与该圆直径的比值)“割圆术”就是以“圆内接正多边形的面积”,来无限逼近“圆面积”,刘徽形容他的“割圆术”说:割之弥细,所失弥少,割之又割,以至于不可割,则与圆合体,而无所失矣.刘徽计算圆周率是从正六边形开始的,易知圆的内接正六边形可分为六个全等的正三角形,每个三角形的边长均为圆的半径R.此时圆内接正六边形的周长为6R,如果将圆内接正六边形的周长等同于圆的周长,可得圆周率为3.当正十二边形内接于圆时,如果按照上述方法计算,可得圆周率为_____.(参考数据:sinl5°=0.26)
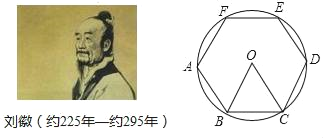
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com