
科目: 来源: 题型:
【题目】当m是何值时,关于x的方程(m2+2)x2+(m﹣1)x﹣4=3x2
(1)是一元二次方程;
(2)是一元一次方程;
(3)若x=﹣2是它的一个根,求m的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,将边长为2cm的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△A′B′C′,若两个三角形重叠部分的面积为1cm2,则它移动的距离AA′等于( )

A. 0.5cm B. 1cm C. 1.5cm D. 2cm
查看答案和解析>>
科目: 来源: 题型:
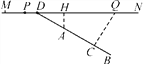
【题目】如图,MN表示一段笔直的高架道路,线段AB表示高架道路旁的一排居民楼,已知点A到MN的距离为15米,BA的延长线与MN相交于点D,且∠BDN=30°,假设汽车在高速道路上行驶时,周围39米以内会受到噪音(XRS)的影响.
(1)过点A作MN的垂线,垂足为点H,如果汽车沿着从M到N的方向在MN上行驶,当汽车到达点P处时,噪音开始影响这一排的居民楼,那么此时汽车与点H的距离为多少米?
(2)降低噪音的一种方法是在高架道路旁安装隔音板,当汽车行驶到点Q时,它与这一排居民楼的距离QC为39米,那么对于这一排居民楼,高架道路旁安装的隔音板至少需要多少米长?(精确到1米)(参考数据:![]() ≈1.7)
≈1.7)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知AB是⊙O的直径,点C,D在⊙O上,且AB=5,BC=3.
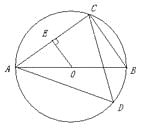
(1) 求sin∠BAC的值;
(2) 如果OE⊥AC, 垂足为E,求OE的长;
(3) 求tan∠ADC的值.(结果保留根号)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,AB,BC是⊙O的弦,∠B=60°,点O在∠B内,点D为![]() 上的动点,点M,N,P分别是AD,DC,CB的中点.若⊙O的半径为2,则PN+MN的长度的最大值是( )
上的动点,点M,N,P分别是AD,DC,CB的中点.若⊙O的半径为2,则PN+MN的长度的最大值是( )

A. ![]()
B. ![]()
C. ![]()
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,要在宽为22米的九州大道两边安装路灯,路灯的灯臂CD长2米,且与灯柱BC成120°角,路灯采用圆锥形灯罩,灯罩的轴线DO与灯臂CD垂直,当灯罩的轴线DO通过公路路面的中心线时照明效果最佳,此时,路灯的灯柱BC高度应该设计为( )

A. (11﹣2![]() )米 B. (11
)米 B. (11![]() ﹣2
﹣2![]() )米 C. (11﹣2
)米 C. (11﹣2![]() )米 D. (11
)米 D. (11![]() ﹣4)米
﹣4)米
查看答案和解析>>
科目: 来源: 题型:
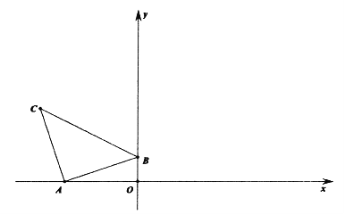
【题目】如图,在平面直角坐标系中有Rt△ABC,∠BAC=90°,AB=AC,A(-3,0),B(0,1),C(m,n)。
(1)请直接写出C点坐标。
(2)将△ABC 沿x轴的正方向平移t个单位,![]() 、
、![]() 两点的对应点、正好落在反比例函数
两点的对应点、正好落在反比例函数![]() 在第一象限内图象上。请求出t,k的值。
在第一象限内图象上。请求出t,k的值。
(3)在(2)的条件下,问是否存x轴上的点M和反比例函数![]() 图象上的点N,使得以
图象上的点N,使得以![]() 、
、![]() 、M、N为顶点的四边形构成平行四边形?如果存在,请求出所有满足条件的点M和点N的坐标;如果不存在,请说明理由。
、M、N为顶点的四边形构成平行四边形?如果存在,请求出所有满足条件的点M和点N的坐标;如果不存在,请说明理由。
查看答案和解析>>
科目: 来源: 题型:
【题目】一司机驾驶汽车从甲地去乙地,以80千米/小时的平均速度用6小时到达目的地.
(1)当他按原路匀速返回时,求汽车速度v(千米/小时)与时间t(小时)之间的函数关系式;
(2)如果该司机匀速返回时,用了4.8小时,求返回时的速度;
(3)若返回时,司机全程走高速公路,且匀速行驶,根据规定:最高车速不得超过每小时120公里,最低车速不得低于每小时60公里,试问返程时间的范围是多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在左边托盘A(固定)中放置一个生物,在右边托盘B(可左右移动)中放置一定重量的砝码,可使得仪器左右平衡,改变托盘B与支撑点M的跳高,记录相应的托盘B中的砝码质量,得到下表:
托盘B与点M的距离x(cm) | 10 | 15 | 20 | 25 | 30 |
托盘B中的砝码质量y(g) | 30 | 20 | 15 | 12 | 10 |
(1)把上表中(x,y)的各级对应值作为点的坐标,在如图所示的平面直角坐标系中描出其余的点,并用一条光滑的曲线连接起来,观察所画的图象,猜想y与x的函数关系,求出该函数关系式.
(2)当托盘B向左移动(不能超过点M)时,应往托盘B中添加砝码还是减少砝码?为什么?

查看答案和解析>>
科目: 来源: 题型:
【题目】为了预防“甲型H1N1”,某校对教室采用药薰消毒法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(mg)与时间x(min)成正比例,药物燃烧后,y与x成反比例,如图所示,现测得药物8min燃毕,此时室内空气每立方米的含药量为6mg,请你根据题中提供的信息,解答下列问题:
(1)药物燃烧时,求y关于x的函数关系式?自变量x的取值范围是什么?药物燃烧后y与x的函数关系式呢?
(2)研究表明,当空气中每立方米的含药量低于1.6mg时,生方可进教室,那么从消毒开始,至少需要几分钟后,生才能进入教室?
(3)研究表明,当空气中每立方米的含药量不低于3mg且持续时间不低于10min时,才能杀灭空气中的毒,那么这次消毒是否有效?为什么?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com