
科目: 来源: 题型:
【题目】对于钝角α,定义它的三角函数值如下:sinα=sin (180°-α),cosα=-cos (180°-α);若一个三角形的三个内角的比是1∶1∶4,A,B是这个三角形的两个顶点,sinA,cosB是方程4x2-mx-1=0的两个不相等的实数根,求m的值及∠A和∠B的大小.
查看答案和解析>>
科目: 来源: 题型:
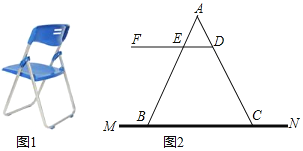
【题目】如图1是一种折叠椅,忽略其支架等的宽度,得到他的侧面简化结构图![]() 图
图![]() ,支架与坐板均用线段表示,若座板DF平行于地面MN,前支撑架AB与后支撑架AC分别与座板DF交于点E、D,现测得
,支架与坐板均用线段表示,若座板DF平行于地面MN,前支撑架AB与后支撑架AC分别与座板DF交于点E、D,现测得![]() 厘米,
厘米, ![]() 厘米,
厘米, ![]() .
.
![]() 求椅子的高度
求椅子的高度![]() 即椅子的座板DF与地面MN之间的距离
即椅子的座板DF与地面MN之间的距离![]() 精确到1厘米
精确到1厘米![]()
![]() 求椅子两脚B、C之间的距离
求椅子两脚B、C之间的距离![]() 精确到1厘米
精确到1厘米![]() 参考数据:
参考数据: ![]()
查看答案和解析>>
科目: 来源: 题型:
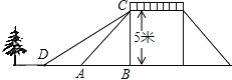
【题目】如图,某公园内有座桥,桥的高度是5米,CB⊥DB,坡面AC的倾斜角为45°,为方便老人过桥,市政部门决定降低坡度,使新坡面DC的坡度为i= ![]() :3.若新坡角外需留下2米宽的人行道,问离原坡角(A点处)6米的一棵树是否需要移栽?(参考数据:
:3.若新坡角外需留下2米宽的人行道,问离原坡角(A点处)6米的一棵树是否需要移栽?(参考数据: ![]() ≈1.414,
≈1.414, ![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目: 来源: 题型:
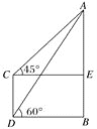
【题目】如图,某电视塔AB和楼CD的水平距离为100 m,从楼顶C处及楼底D处测得塔顶A的仰角分别为45°和60°,试求塔高为__________,楼高为__________.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知直线y=-2x经过点P(-2,m),点P关于y轴的对称点P′在反比例函数![]() (
(![]() )的图象上.
)的图象上.
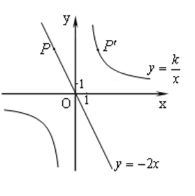
(1)求m的值;
(2)直接写出点P′的坐标;
(3)求反比例函数的解析式.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:抛物线y=mx2+(m﹣2)x﹣2m+2(m≠0).
(1)求证:抛物线与x轴有交点;
(2)若抛物线与x轴交于点A(x1,0),B(x2,0),点A在点B的右侧,且x1+2x2=1.
①求m的值;
②点P在抛物线上,点G(n,﹣![]() n﹣
n﹣![]() ),求PG的最小值.
),求PG的最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】(问题情境)
(1)古希腊著名数学家欧几里得在《几何原本》提出了射影定理,又称“欧几里德定理”:在直角三角形中,斜边上的高是两条直角边在斜边射影的比例中项,每一条直角边又是这条直角边在斜边上的射影和斜边的比例中项.射影定理是数学图形计算的重要定理.
其符号语言是:如图1,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,则:(1)CD = AD·BD, (2)AC = AB·AD, (3)BC=AB·BD;请你证明定理中的结论(2)BC=AB·BD.
(结论运用)
(2)如图2,正方形ABCD的边长为6,点O是对角线AC、BD的交点,点E在CD上,过点C作CF⊥BE,垂足为F,连接OF,
①求证:△BOF∽△BED;
②若![]() ,求OF的长.
,求OF的长.
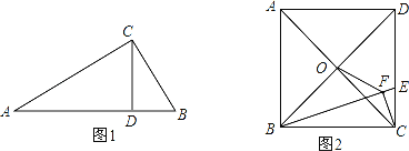
查看答案和解析>>
科目: 来源: 题型:
【题目】阳光市场某个体商户购进某种电子产品,每个进价是50元.调查发现,当售价是80元时,平均一周可卖出160个,而当售价每降低2元时,平均一周可多卖出20个.若设每个电子产品降价x元,
(1)根据题意,填表:
进价(元) | 售价(元) | 每件利润(元) | 销量(个) | 一周总利润(元) | |
降价前 | 50 | 80 | 30 | 160 |
|
降价后 | 50 |
(2)若商户计划每周盈利5200元,且尽量减少库存,则应降价多少元?
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:二次函数![]()
![]() 中的
中的![]() 和
和![]() 满足下表:
满足下表:
| … |
| 0 | 1 | 2 | 3 | … |
| … | 3 | 0 |
| 0 | m | … |
(1) 观察上表可求得![]() 的值为________;
的值为________;
(2) 试求出这个二次函数的解析式;
(3) 若点A(n+2,y1),B(n,y2)在该抛物线上,且y1>y2,请直接写出n的取值范围.
查看答案和解析>>
科目: 来源: 题型:
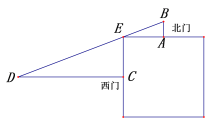
【题目】我国古代数学著作《九章算术》中记载了一个问题:“今有邑方不知大小,各开中门,出北门三十步有木,出西门七百五十步见木,问:邑方几何?” .其大意是:如图,一座正方形城池,A为北门中点,从点A往正北方向走30步到B出有一树木,C为西门中点,从点C往正西方向走750步到D处正好看到B处的树木,求正方形城池的边长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com