
科目: 来源: 题型:
【题目】对于平面直角坐标系xOy中的点P,Q和图形G,给出如下定义:点P,Q都在图形G上,且将点P的横坐标与纵坐标互换后得到点Q,则称点P,Q是图形G的一对“关联点”.例如,点P(1,2)和点Q(2,1)是直线y=﹣x+3的一对关联点.
(1)请写出反比例函数y=![]() 的图象上的一对关联点的坐标: ;
的图象上的一对关联点的坐标: ;
(2)抛物线y=x2+bx+c的对称轴为直线x=1,与y轴交于点C(0,﹣1).点A,B是抛物线y=x2+bx+c的一对关联点,直线AB与x轴交于点D(1,0).求A,B两点坐标.
(3)⊙T的半径为3,点M,N是⊙T的一对关联点,且点M的坐标为(1,m)(m>1),请直接写出m的取值范围.
查看答案和解析>>
科目: 来源: 题型:
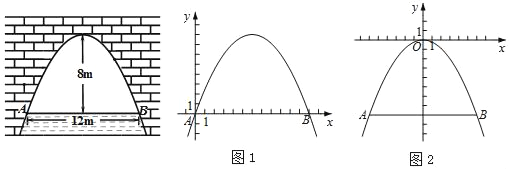
【题目】如图是抛物线型拱桥,当拱顶离水面8m时,水面宽AB为12m.当水面上升6m时达到警戒水位,此时拱桥内的水面宽度是多少m?
下面给出了解决这个问题的两种方法,请补充完整:
方法一:如图1,以点A为原点,AB所在直线为x轴,建立平面直角坐标系xOy,
此时点B的坐标为( , ),抛物线的顶点坐标为( , ),
可求这条抛物线所表示的二次函数的解析式为 .
当y=6时,求出此时自变量x的取值,即可解决这个问题.
方法二:如图2,以抛物线顶点为原点,对称轴为y轴,建立平面直角坐标系xOy,
这时这条抛物线所表示的二次函数的解析式为 .
当y= 时,求出此时自变量x的取值为 ,即可解决这个问题.
查看答案和解析>>
科目: 来源: 题型:
【题目】中国古代有着辉煌的数学成就,《周髀算经》,《九章算术》,《海岛算经》,《孙子算经》等是我国古代数学的重要文献.
(1)小聪想从这4部数学名著中随机选择1部阅读,则他选中《九章算术》的概率为 ;
(2)某中学拟从这4部数学名著中选择2部作为“数学文化”校本课程学习内容,求恰好选中《九章算术》和《孙子算经》的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】下面是小芸设计的“过圆外一点作已知圆的切线”的尺规作图过程.
已知:⊙O及⊙O外一点P.
求作:⊙O的一条切线,使这条切线经过点P.
作法:①连接OP,作OP的垂直平分线l,
交OP于点A;
②以A为圆心,AO为半径作圆,
交⊙O于点M;
③作直线PM,则直线PM即为⊙O的切线.
根据小芸设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明:
证明:连接OM,
由作图可知,A为OP中点,
∴OP为⊙A直径,
∴∠OMP= °,( )(填推理的依据)
即OM⊥PM.
又∵点M在⊙O上,
∴PM是⊙O的切线.( )(填推理的依据)
查看答案和解析>>
科目: 来源: 题型:
【题目】下表显示了同学们用计算机模拟随机投针实验的某次实验的结果.
投针次数n | 1000 | 2000 | 3000 | 4000 | 5000 | 10000 | 20000 |
针与直线相交的次数m | 454 | 970 | 1430 | 1912 | 2386 | 4769 | 9548 |
针与直线相交的频率p=
| 0.454 | 0.485 | 0.4767 | 0.478 | 0.4772 | 0.4769 | 0.4774 |
下面有三个推断:
①投掷1000次时,针与直线相交的次数是454,针与直线相交的概率是0.454;
②随着实验次数的增加,针与直线相交的频率总在0.477附近,显示出一定的稳定性,可以估计针与直线相交的概率是0.477;
③若再次用计算机模拟此实验,则当投掷次数为10000时,针与直线相交的频率一定是0.4769.
其中合理的推断的序号是:_____.
查看答案和解析>>
科目: 来源: 题型:
【题目】心理学家发现:课堂上,学生对概念的接受能力s与提出概念的时间t(单位:min)之间近似满足函数关系s=at2+bt+c(a≠0),s值越大,表示接受能力越强.如图记录了学生学习某概念时t与s的三组数据,根据上述函数模型和数据,可推断出当学生接受能力最强时,提出概念的时间为( )
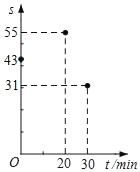
A. 8min B. 13min C. 20min D. 25min
查看答案和解析>>
科目: 来源: 题型:
【题目】已知近视眼镜的度数y(度)与镜片焦距x(米)之间成如图所示的反比例函数关系,则眼镜度数y与镜片焦距x之间的函数解析式为( )

A. y=200x B. y=![]() C. y=100x D. y=
C. y=100x D. y=![]()
查看答案和解析>>
科目: 来源: 题型:
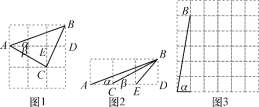
【题目】数学老师布置了这样一个问题:如果α,β都为锐角,且tanα=![]() ,tanβ=
,tanβ=![]() .求α+β的度数.甲、乙两位同学想利用正方形网格构图来解决问题.他们分别设计了图1和图2.
.求α+β的度数.甲、乙两位同学想利用正方形网格构图来解决问题.他们分别设计了图1和图2.
(1)请你分别利用图1,图2求出α+β的度数,并说明理由;
(2)请参考以上思考问题的方法,选择一种方法解决下面问题:
如果α,β都为锐角,当tanα=5,tanβ=![]() 时,在图3的正方形网格中,利用已作出的锐角α,画出∠MON,使得∠MON=α-β.求出α-β的度数,并说明理由.
时,在图3的正方形网格中,利用已作出的锐角α,画出∠MON,使得∠MON=α-β.求出α-β的度数,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
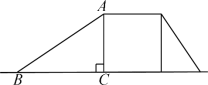
【题目】如图所示是某公园“六一”前新增设的一台滑梯.该滑梯的高度AC=2 m,滑梯着地点B与梯架之间的距离BC=4m.
(1)求滑梯AB的长(精确到0.1 m);
(2)若规定滑梯的倾斜角(∠ABC)不超过45°属于安全,请通过计算说明这架滑梯的倾斜角是否符合要求.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com