
科目: 来源: 题型:
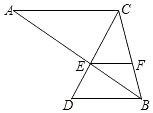
【题目】如图,已知AC∥BD,AB和CD相交于点E,AC=6,BD=4,F是BC上一点,S△BEF:S△EFC=2:3.
(1)求EF的长;
(2)如果△BEF的面积为4,求△ABC的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】小红家的阳台上放置了一个晒衣架如图①.图②是晒衣架的侧面示意图,立杆AB,CD相交于点O,B,D两点立于地面.经测量:AB=CD=136 cm,OA=OC=51 cm,OE=OF=34 cm,现将晒衣架完全稳固张开,扣链EF成一条线段,且EF=32 cm.垂挂在衣架上的连衣裙总长度小于________cm时,连衣裙才不会拖落到地面上.

查看答案和解析>>
科目: 来源: 题型:
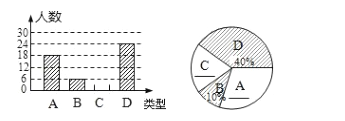
【题目】学校调查了某班同学上学的方式有四种:骑自行车、步行、乘坐公交车和家长接送(分别用A、B、C、D表示),根据调查结果绘制成如图所示的条形统计图和扇形统计图(未完成),请集合图中所给信息解答下列问题:
(1)这个班级学生共有多少人?
(2)将两幅不完整的图补充完整;
(3)求扇形统计图中C所对圆心角的度数;
(4)已知步行上学的同学中有3名女同学,学校将从步行上学的同学中随机选出2名同学参加交通安全知识培训,求所选2名同学恰好是一男一女的概率.
查看答案和解析>>
科目: 来源: 题型:
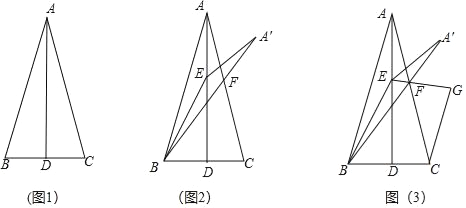
【题目】已知:AD是△ABC的高,且BD=CD.
(1)如图1,求证:∠BAD=∠CAD;
(2)如图2,点E在AD上,连接BE,将△ABE沿BE折叠得到△A′BE,A′B与AC相交于点F,若BE=BC,求∠BFC的大小;
(3)如图3,在(2)的条件下,连接EF,过点C作CG⊥EF,交EF的延长线于点G,若BF=10,EG=6,求线段CF的长.
查看答案和解析>>
科目: 来源: 题型:
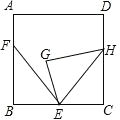
【题目】如图,正方形 ABCD 中,点 E,F 分别在 BC 和 AB 上,BE=3,AF=2,BF=4,将△ BEF 绕点 E 顺时针旋转,得到△GEH,当点 H 落在 CD 边上时,F,H 两点之间的距离为_____.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,抛物线![]() 的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.
的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.
(1)求A、B、C的坐标;
(2)点M为线段AB上一点(点M不与点A、B重合),过点M作x轴的垂线,与直线AC交于点E,与抛物线交于点P,过点P作PQ∥AB交抛物线于点Q,过点Q作QN⊥x轴于点N.若点P在点Q左边,当矩形PQMN的周长最大时,求△AEM的面积;
(3)在(2)的条件下,当矩形PMNQ的周长最大时,连接DQ.过抛物线上一点F作y轴的平行线,与直线AC交于点G(点G在点F的上方).若FG=![]() DQ,求点F的坐标.
DQ,求点F的坐标.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,BC是路边坡角为30°,长为10米的一道斜坡,在坡顶灯杆CD的顶端D处有一探射灯,射出的边缘光线DA和DB与水平路面AB所成的夹角∠DAN和∠DBN分别是37°和60°(图中的点A、B、C、D、M、N均在同一平面内,CM∥AN).
(1)求灯杆CD的高度;
(2)求AB的长度(结果精确到0.1米).(参考数据:![]() =1.73.sin37°≈060,cos37°≈0.80,tan37°≈0.75)
=1.73.sin37°≈060,cos37°≈0.80,tan37°≈0.75)

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,将矩形ABCO放在直角坐标系中,其中顶点B的坐标为(10, 8),E是BC边上一点将△ABE沿AE折叠,点B刚好与OC边上点D重合,过点E的反比例函数y=![]() 的图象与边AB交于点F, 则线段AF的长为( )
的图象与边AB交于点F, 则线段AF的长为( )

A. ![]() B. 2 C.
B. 2 C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
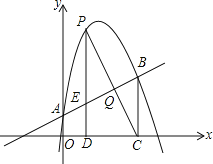
【题目】如图,抛物线y=ax2+bx+1经过点(2,6),且与直线y=![]() x+1相交于A,B两点,点A在y轴上,过点B作BC⊥x轴,垂足为点C(4,0).
x+1相交于A,B两点,点A在y轴上,过点B作BC⊥x轴,垂足为点C(4,0).
(1)求抛物线的解析式;
(2)若P是直线AB上方该抛物线上的一个动点,过点P作PD⊥x轴于点D,交AB于点E,求线段PE的最大值;
(3)在(2)的条件,设PC与AB相交于点Q,当线段PC与BE相互平分时,请求出点Q的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com