
科目: 来源: 题型:
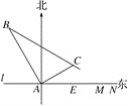
【题目】在某飞机场东西方向的地面l上有一长为1 km的飞机跑道MN(如图),在跑道MN的正西端14.5千米处有一观察站A.某时刻测得一架匀速直线降落的飞机位于点A的北偏西30°,且与点A相距15千米的B处;经过1分钟,又测得该飞机位于点A的北偏东60°,且与点A相距5![]() 千米的C处.
千米的C处.
(1)该飞机航行的速度是多少千米/小时?(结果保留根号)
(2)如果该飞机不改变航向继续航行,那么飞机能否降落在跑道MN之间?请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】同学们,在我们进入高中以后,将还会学到下面三角函数公式:
sin (α-β)=sinαcosβ-cosαsinβ,
cos (α-β)=cosαcosβ+sinαsinβ
例:sin 15°=sin (45°-30°)=sin 45°cos 30°-cos 45°sin 30°=![]()
(1)试仿照例题,求出cos 15°的准确值;
(2)我们知道,tanα=![]() ,试求出tan 15°的准确值.
,试求出tan 15°的准确值.
查看答案和解析>>
科目: 来源: 题型:
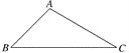
【题目】三角形中有3个角、3条边共6个元素,由其中的已知元素,求出所有未知元素的过程,叫做解三角形.
已知△ABC中,AB=![]() ,∠B=45°,BC=1+
,∠B=45°,BC=1+![]() ,解△ABC.
,解△ABC.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,2分别是某款篮球架的实物图与示意图,已知底座BC=0.60米,底座BC与支架AC所成的角∠ACB=75°,支架AF的长为2.50米,篮板顶端F点到篮框D的距离FD=1.35米,篮板底部支架HE与支架AF所成的角∠FHE=60°,求篮框D到地面的距离(精确到0.01米)(参考数据:cos75°≈0.2588,sin75°≈0.9659,tan75°≈3.732,![]() ≈1.732,
≈1.732,![]() ≈1.414)
≈1.414)

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,一垂直于地面的灯柱AB被一钢筋CD固定,CD与地面成45°夹角(∠CDB=45°),在C点上方2米处加固另一条钢线ED,ED与地面成53°夹角(∠EDB=53°),那么钢线ED的长度约为多少米?(结果精确到1米,参考数据:sin53°≈0.80,cos53°≈0.60,tan53°≈1.33)

查看答案和解析>>
科目: 来源: 题型:
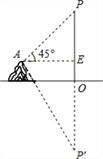
【题目】在湖边高出水面50m的山顶A处看见一艘飞艇停留在湖面上空某处,观察到飞艇底部标志P处的仰角为45°,又观其在湖中之像的俯角为60°,则飞艇底部P距离湖面的高度为(参考等式: ![]() )( )
)( )
A. 25![]() +75 B. 50
+75 B. 50![]() +50 C. 75
+50 C. 75![]() +75 D. 50
+75 D. 50![]() +100
+100
查看答案和解析>>
科目: 来源: 题型:
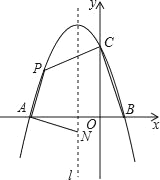
【题目】如图,抛物线y=ax2+bx+c与x轴交于点A和点B(1,0),与y轴交于点C(0,3),其对称轴l为x=﹣1.
(1)求抛物线的解析式并写出其顶点坐标;
(2)若动点P在第二象限内的抛物线上,动点N在对称轴l上.
①当PA⊥NA,且PA=NA时,求此时点P的坐标;
②当四边形PABC的面积最大时,求四边形PABC面积的最大值及此时点P的坐标.
查看答案和解析>>
科目: 来源: 题型:
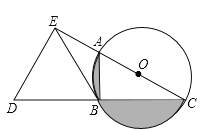
【题目】如图,AC为⊙O的直径,B为⊙O上一点,∠ACB=30°,延长CB至点D,使得CB=BD,过点D作DE⊥AC,垂足E在CA的延长线上,连接BE.
(1)求证:BE是⊙O的切线;
(2)当BE=3时,求图中阴影部分的面积.
查看答案和解析>>
科目: 来源: 题型:
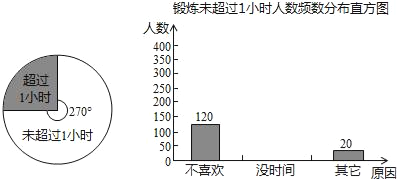
【题目】国家教委规定“中小学生每天在校体育活动时间不低于1小时”.为此某中学为了了解学生体育活动情况,随机调查了720名毕业班学生,调查内容是:“每天锻炼是否超过1小时及未超过1小时的原因”,所得的数据制成了的扇形统计图和频数分布直方图.根据图示,解答下列问题:
(1)若在被调查的学生中随机选出一名学生测试其体育成绩,选出的恰好是“每天锻炼超过1小时”的学生的概率是多少?
(2)“没时间”的人数是多少?并补全频数分布直方图;
(3)2010年这个地区初中毕业生约为3.2万人,按此调查,可以估计2010年这个地区初中毕业生中每天锻炼未超过1小时的学生约有多少万人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com