
科目: 来源: 题型:
【题目】根据下列要求,解答相关问题:
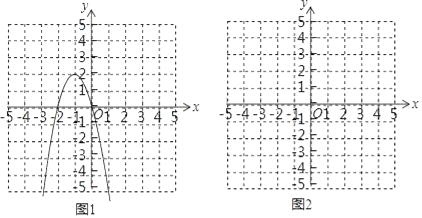
(1)请补全以下求不等式﹣2x2﹣4x≥0的解集的过程
①构造函数,画出图象:
根据不等式特征构造二次函数y=﹣2x2﹣4x;抛物线的对称轴x=﹣1,开口向下,顶点(﹣1,2)与x轴的交点是(0,0),(﹣2,0),用三点法画出二次函数y=﹣2x2﹣4x的图象如图1所示;
②数形结合,求得界点:
当y=0时,求得方程﹣2x2﹣4x=0的解为 ;
③借助图象,写出解集:
由图象可得不等式﹣2x2﹣4x≥0的解集为 .
(2)利用(1)中求不等式解集的方法步骤,求不等式x2﹣2x+1<4的解集.
①构造函数,画出图象;
②数形结合,求得界点;
③借助图象,写出解集.
(3)参照以上两个求不等式解集的过程,借助一元二次方程的求根公式,直接写出关于x的不等式ax2+bx+c>0(a>0)的解集.
查看答案和解析>>
科目: 来源: 题型:
【题目】某中学为丰富学生的校园生活,准备从体育用品商店一次性购买若干个足球和篮球(每个足球的价格相同,每个篮球的价格相同),若购买3个足球和2个篮球共需310元,购买2个足球和5个篮球共需500元。
(1)求购买一个足球、一个篮球各需多少元?
(2)根据学校实际情况,需从体育用品商店一次性购买足球和篮球共96个,要求购买足球和篮球的总费用不超过5720元,这所中学最多可以购买多少个篮球?
查看答案和解析>>
科目: 来源: 题型:
【题目】(9分)如图,AB是半圆O的直径,点P是半圆上不与点A、B重合的一个动点,延长BP到点C,使PC=PB,D是AC的中点,连接PD,PO.
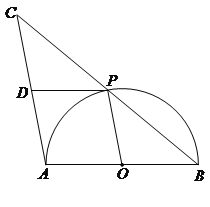
(1)求证:△CDP≌△POB;
(2)填空:
① 若AB=4,则四边形AOPD的最大面积为 ;
② 连接OD,当∠PBA的度数为 时,四边形BPDO是菱形.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,在正方形ABCD中,点E,F分别是边BC,AB上的点,且CE=BF.连接DE,过点E作EG⊥DE,使EG=DE,连接FG,FC.
(1)请判断:FG与CE的关系是___;
(2)如图2,若点E,F分别是边CB,BA延长线上的点,其它条件不变,(1)中结论是否仍然成立?请作出判断并给予证明;
(3)如图3,若点E,F分别是边BC,AB延长线上的点,其它条件不变,(1)中结论是否仍然成立?请直接写出你的判断.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在大楼AB的正前方有一斜坡CD,CD=4米,坡角∠DCE=30°,小红在斜坡下的点C处测得楼顶B的仰角为60°,在斜坡上的点D处测得楼顶B的仰角为45°,其中点A、C、E在同一直线上.
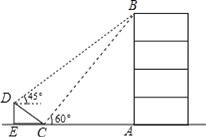
(1)求斜坡CD的高度DE;
(2)求大楼AB的高度(结果保留根号)
查看答案和解析>>
科目: 来源: 题型:
【题目】在信息快速发展的社会,“信息消费”已成为人们生活的重要组成部分.某高校组织课外小组在郑州市的一个社区随机抽取部分家庭,调查每月用于信息消费的金额,根据数据整理成如图所示的不完整统计表和统计图.已知A,B两组户数频数直方图的高度比为1:5.
月信息消费额分组统计表
组别 | 消费额(元) |
A | 10≤x<100 |
B | 100≤x<200 |
C | 20≤x<300 |
D | 300≤x<400 |
E | x≥400 |
请结合图表中相关数据解答下列问题:
(1)这次接受调查的有 户;
(2)在扇形统计图中,“E”所对应的圆心角的度数是 ;
(3)请你补全频数直方图;
(4)若该社区有2000户住户,请估计月信息消费额不少于200元的户数是多少?

查看答案和解析>>
科目: 来源: 题型:
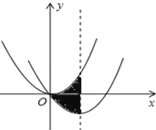
【题目】如图,在平面直角坐标系中,抛物线y=![]() x2经过平移得到抛物线y=ax2+bx,其对称轴与两段抛物线所围成的阴影部分的面积为
x2经过平移得到抛物线y=ax2+bx,其对称轴与两段抛物线所围成的阴影部分的面积为![]() ,则a、b的值分别为( )
,则a、b的值分别为( )
A. ![]() ,
,![]() B.
B. ![]() ,﹣
,﹣![]() C.
C. ![]() ,﹣
,﹣![]() D. ﹣
D. ﹣![]() ,
,![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,菱形OABC的一边OA在x轴上,将菱形OABC绕原点O顺时针旋转75°至OA’B’C’的位置.若OB=![]() ,∠C=120°,则点B’的坐标为( )
,∠C=120°,则点B’的坐标为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com