
科目: 来源: 题型:
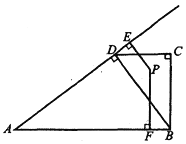
【题目】如图,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() .点
.点![]() 在
在![]() 的边上或内部运动,过点
的边上或内部运动,过点![]() 分别向边
分别向边![]() 、
、![]() 所在直线作垂线,交射线
所在直线作垂线,交射线![]() 于点
于点![]() ,交边
,交边![]() 于点
于点![]() .
.
(1)求边![]() 的长.
的长.
(2)求线段![]() 的取值范围.
的取值范围.
(3)当点![]() 在
在![]() 的边上运动时,若
的边上运动时,若![]() ,直接写出线段
,直接写出线段![]() 的长.
的长.
查看答案和解析>>
科目: 来源: 题型:
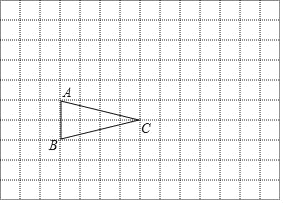
【题目】如图,方格纸中每个小正方形的边长均为1,△ABC的三个顶点均在小正方形的顶点上.
(1)请在方格纸上建立平面直角坐标系,使点A、C的坐标分别为(2,3)、(6,2),并写出点B的坐标;
(2)以原点O为位似中心,在第一象限内将△ABC放大,相似比为2,画出放大后的△A'B'C';
(3)直接写出B′C′与AC的交点坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线 y=ax2﹣5ax+c 交 x 轴于点 A,点 A 的坐标为(4,0).
(1)用含 a 的代数式表示 c.
(2)当 a=![]() 时,求 x 为何值时 y 取得最小值,并求出 y 的最小值.
时,求 x 为何值时 y 取得最小值,并求出 y 的最小值.
(3)当 a=![]() 时,求 0≤x≤6 时 y 的取值范围.
时,求 0≤x≤6 时 y 的取值范围.
(4)已知点 B 的坐标为(0,3),当抛物线的顶点落在△AOB 外接圆内部时,直接写出 a的取值范围.
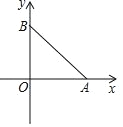
查看答案和解析>>
科目: 来源: 题型:
【题目】某游乐园有一个直径为16米的圆形喷水池,喷水池的周边有一圈喷水头,喷出的水柱为抛物线,在距水池中心3米处达到最高,高度为5米,且各方向喷出的水柱恰好在喷水池中心的装饰物处汇合.如图所示,以水平方向为x轴,喷水池中心为原点建立直角坐标系.
(1)求水柱所在抛物线(第一象限部分)的函数表达式;
(2)王师傅在喷水池内维修设备期间,喷水管意外喷水,为了不被淋湿,身高1.8米的王师傅站立时必须在离水池中心多少米以内?
(3)经检修评估,游乐园决定对喷水设施做如下设计改进:在喷出水柱的形状不变的前提下,把水池的直径扩大到32米,各方向喷出的水柱仍在喷水池中心保留的原装饰物(高度不变)处汇合,请探究扩建改造后喷水池水柱的最大高度.

查看答案和解析>>
科目: 来源: 题型:
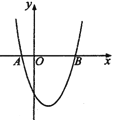
【题目】如图,在平面直角坐标系中,抛物线![]() 与
与![]() 轴相交于
轴相交于![]() 、
、![]() 两点.若在抛物线上有且只有三个不同的点
两点.若在抛物线上有且只有三个不同的点![]() 、
、![]() 、
、![]() ,使得
,使得![]() 、
、![]() 、
、![]() 的面积都等于
的面积都等于![]() ,则
,则![]() 的值是( )
的值是( )
A. 6 B. 8 C. 12 D. 16
查看答案和解析>>
科目: 来源: 题型:
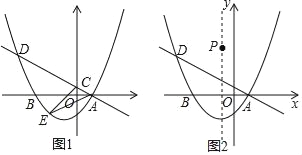
【题目】如图1,在平面直角坐标系xOy中,抛物线y=ax2+bx﹣![]() 与x轴交于点A(1,0)和点B(﹣3,0).绕点A旋转的直线l:y=kx+b1交抛物线于另一点D,交y轴于点C.
与x轴交于点A(1,0)和点B(﹣3,0).绕点A旋转的直线l:y=kx+b1交抛物线于另一点D,交y轴于点C.
(1)求抛物线的函数表达式;
(2)当点D在第二象限且满足CD=5AC时,求直线l的解析式;
(3)在(2)的条件下,点E为直线l下方抛物线上的一点,直接写出△ACE面积的最大值;
(4)如图2,在抛物线的对称轴上有一点P,其纵坐标为4,点Q在抛物线上,当直线l与y轴的交点C位于y轴负半轴时,是否存在以点A,D,P,Q为顶点的平行四边形?若存在,请直接写出点D的横坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
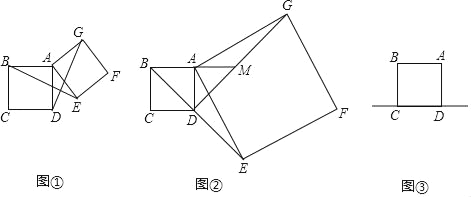
【题目】已知正方形ABCD的边长为2,作正方形AEFG(A,E,F,G四个顶点按逆时针方向排列),连接BE、GD,
(1)如图①,当点E在正方形ABCD外时,线段BE与线段DG有何关系?直接写出结论;
(2)如图②,当点E在线段BD的延长线上,射线BA与线段DG交于点M,且DG=2DM时,求边AG的长;
(3)如图③,当点E在正方形ABCD的边CD所在的直线上,直线AB与直线DG交于点M,且DG=4DM时,直接写出边AG的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】为迎接“全民阅读日“系列活动,某校围绕学生日人均阅读时间这一问题,对八年级学生进行随机抽样调查.如图是根据调查结果绘制成的统计图(不完整),请你根据图中提供的信息解答下列问题:
(1)本次共抽查了八年级学生多少人;
(2)请直接将条形统计图补充完整;
(3)在扇形统计图中,11.5小时对应的圆心角是多少度;
(4)根据本次抽样调查,估计全市50000名八年级学生日人均阅读时间状况,其中在0.51.5小时的有多少人?

查看答案和解析>>
科目: 来源: 题型:
【题目】随着信息技术的快速发展,“互联网+”渗透到我们日常生活的各个领域,网上在线学习交流已不再是梦,现有某教学网站策划了A,B两种上网学习的月收费方式:
收费方式 | 月使用费/元 | 包时上网时间/h | 超时费/(元/min) |
A | 7 | 25 | 0.01 |
B | m | n | 0.01 |
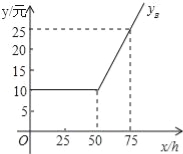
设每月上网学习时间为x小时,方案A,B的收费金额分别为yA,yB.
(1)如图是yB与x之间函数关系的图象,请根据图象填空:m= ;n=
(2)写出yA与x之间的函数关系式.
(3)选择哪种方式上网学习合算,为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com