
科目: 来源: 题型:
【题目】如图,二次函数y=x2﹣2x﹣3的图象与x轴交于A、B两点,与y轴交于点C,则下列说法错误的是( )
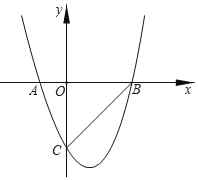
A. AB=4
B. ∠ABC=45°
C. 当x>0时,y<﹣3
D. 当x>1时,y随x的增大而增大
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系中,抛物线y=ax2﹣2ax﹣3与x轴交于A、B两点(点A在点B左侧),与y轴交于点C,顶点为D,且过点(2,﹣3a).
(1)求抛物线的解析式;
(2)抛物线上是否存在一点P,过点P作PM⊥BD,垂足为点M,PM=2DM?若存在,求点P的坐标;若不存在,说明理由.
(3)在(2)的条件下,求△PMD的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读下面材料:
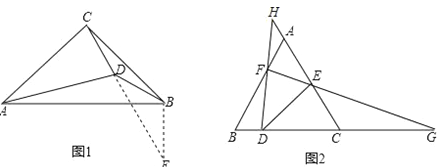
小明遇到这样一个问题:如图1,在△ABC中,∠ACB=90°,AC=BC,在三角形内取一点D,AD=AC,∠CAD=30°,求∠ADB.
小明通过探究发现,∠DAB=∠DCB=15°,BC=AD,这样就具备了一边一角的图形特征,他果断延长CD至点E,使CE=AB,连接EB,造出全等三角形,使问题得到解决.
(1)按照小明思路完成解答,求∠ADB;
(2)参考小明思考问题的方法,解答下列问题:
如图2,△ABC中,AB=AC,点D、E、F分别为BC、AC、AB上一点,连接DE,延长FE、DF分别交BC、CA延长线于点G、H,若∠DHC=∠EDG=2∠G.
①在图中找出与∠DEC相等的角,并加以证明;
②若BG=kCD,猜想DE与DG的数量关系并证明.
查看答案和解析>>
科目: 来源: 题型:
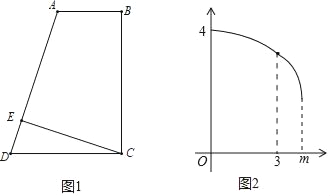
【题目】如图1,在四边形ABCD中,AB∥CD,BC⊥CD,过点C作CE⊥AD于点E,CE=4,△CDE沿射线DA平移,当CE经过点B时,运动停止.设点D的平移距离为x,平移后的三角形与四边形ABCD的重合部分面积为y,y与x的函数图象如图2所示:
(1)图中DE= ;
(2)求BC的长;
(3)求y与x的函数关系式,并直接写出x的取值范围.
查看答案和解析>>
科目: 来源: 题型:
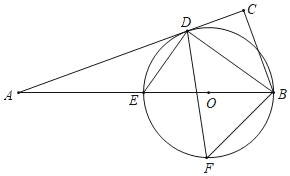
【题目】如图,在△ABC中,∠C=90°,点O为BE上一点,以OB为半径的⊙O交AB于点E,交AC于点D.BD平分∠ABC.
(1)求证:AC为⊙O切线;
(2)点F为![]() 的中点,连接BF,若BC=
的中点,连接BF,若BC=![]() ,BD=8,求⊙O半径及DF的长.
,BD=8,求⊙O半径及DF的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】(发现)x4﹣5x2+4=0是一个一元四次方程.
(探索)根据该方程的特点,通常用“换元法”解方程:
设x2=y,那么x4=y2,于是原方程可变为 .
解得:y1=1,y2= .
当y=1时,x2=1,∴x=±1;
当y= 时,x2= ,∴x= ;
原方程有4个根,分别是 .
(应用)仿照上面的解题过程,求解方程:![]() .
.
查看答案和解析>>
科目: 来源: 题型:
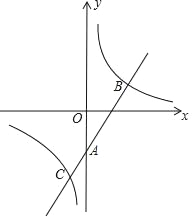
【题目】如图,在平面直角坐标系中,一次函数y1=ax+b(a≠0)的图象与y轴相交于点A,与反比例函数y2=![]() (k≠0)的图象相交于点B(3,2)、C(﹣1,n).
(k≠0)的图象相交于点B(3,2)、C(﹣1,n).
(1)求一次函数和反比例函数的解析式;
(2)根据图象,直接写出y1>y2时x的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】某工厂大门是一抛物线形水泥建筑物(如图),大门地面宽AB=4米,顶部C离地面高度为4.4米.现有一辆满载货物的汽车欲通过大门,货物顶部距地面2.8米,装货宽度为2.4米.请通过计算,判断这辆汽车能否顺利通过大门?

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知等腰三角形ADC,AD=AC,B是线段DC上的一点,连结AB,且有AB=DB.
(1)求证:△ADB∽△CDA;
(2)若DB=2,BC=3,求AD的值.

查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系xOy中,正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…,按如图所示的方式放置.点A1,A2,A3,…,An和点C1,C2,C3,…,Cn分别落在直线y=x+1和x轴上.抛物线L1过点A1,B1,且顶点在直线y=x+1上,抛物线L2过点A2,B2,且顶点在直线y=x+1上,……,按此规律,抛物线Ln过点An,Bn,且顶点也在直线y=x+1上,其中抛物线L2交正方形A1B1C1O的边A1B1于点D1,抛物线L3交正方形A2B2C2C1的边A2B2于点D2,…抛物线Ln+1交正方形AnBnCnCn-1的边AnBn于点Dn(其中n≥1,且n为正整数).
(1)直接写出下列点B1B2,B3的坐标;
(2)写出抛物线L2,L3的解析式,并写出其中一个解析式的求解过程,再猜想抛物线Ln的顶点坐标;
(3)①设A1D1=k1·D1B1,A2D2=k2·D2B2,试判断k1与k2的数量关系并说明理由;
②点D1,D2,…,Dn是否在一条直线上?若是,直接写出这条直线与直线y=x+1的交点坐标;若不是,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com