
科目: 来源: 题型:
【题目】在平面直角坐标系xOy中,过原点O的直线l1与双曲线![]() 的一个交点为A(1,m).
的一个交点为A(1,m).
(1)求直线l1的表达式;
(2)过动点P(n,0)(n>0)且垂直于x轴的直线与直线l1和双曲线![]() 的交点分别为B,C,当点B位于点C上方时,直接写出n的取值范围.
的交点分别为B,C,当点B位于点C上方时,直接写出n的取值范围.
查看答案和解析>>
科目: 来源: 题型:
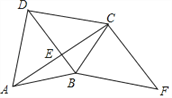
【题目】如图,四边形ABCD的对角线AC⊥BD于点E,AB=BC,F为四边形ABCD外一点,且∠FCA=90°,∠CBF=∠DCB.
(1)求证:四边形DBFC是平行四边形;
(2)如果BC平分∠DBF,∠CDB=45°,BD=2,求AC的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】小明和小亮组成团队参加某科学比赛.该比赛的规则是:每轮比赛一名选手参加,若第一轮比赛得分满60则另一名选手晋级第二轮,第二轮比赛得分最高的选手所在团队取得胜利.为了在比赛中取得更好的成绩,两人在赛前分别作了九次测试,如图为二人测试成绩折线统计图,下列说法合理的是( )
①小亮测试成绩的平均数比小明的高;②小亮测试成绩比小明的稳定;③小亮测试成绩的中位数比小明的高;④小亮参加第一轮比赛,小明参加第二轮比赛,比较合理.
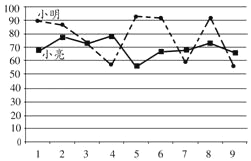
A. ①③B. ①④C. ②③D. ②④
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,抛物线y=ax2﹣5ax+c与坐标轴分别交于点A,C,E三点,其中A(﹣3,0),C(0,4),点B在x轴上,AC=BC,过点B作BD⊥x轴交抛物线于点D,点M,N分别是线段CO,BC上的动点,且CM=BN,连接MN,AM,AN.
(1)求抛物线的解析式及点D的坐标;
(2)当△CMN是直角三角形时,求点M的坐标;
(3)试求出AM+AN的最小值.

查看答案和解析>>
科目: 来源: 题型:
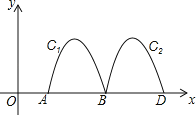
【题目】如图,抛物线y=﹣2x2+8x﹣6与x轴交于点A、B,把抛物线在x轴及其上方的部分记作C1,将C1向右平移得C2,C2与x轴交于点B,D.若直线y=x+m与C1、C2共有3个不同的交点,则m的取值范围是____________.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,AB是⊙O的直径,点C为⊙O上一点,AE和过点C的切线互相垂直,垂足为E,AE交⊙O于点D,直线EC交AB的延长线于点P,连接AC,BC,PB:PC=1:2.

(1)求证:AC平分∠BAD;
(2)探究线段PB,AB之间的数量关系,并说明理由;
(3)若AD=3,求△ABC的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BD相交于点N,连接BM,DN.
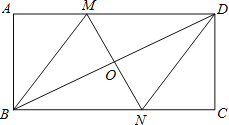
(1)求证:四边形BMDN是菱形;
(2)若AB=4,AD=8,求MD的长
查看答案和解析>>
科目: 来源: 题型:
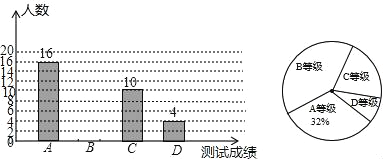
【题目】某中学为了了解九年级学生体能状况,从九年级学生中随机抽取部分学生进行体能测试,测试结果分为A,B,C,D四个等级,并依据测试成绩绘制了如下两幅尚不完整的统计图;
(1)这次抽样调查的样本容量是 ,并补全条形图;
(2)D等级学生人数占被调查人数的百分比为 ,在扇形统计图中C等级所对应的圆心角为 °;
(3)该校九年级学生有1500人,请你估计其中A等级的学生人数.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,己知点A是双曲线y=kx-1(k>0)上的一个动点,连AO并延长交另一分支于点B,以AB为边作等边△ABC,点C在第四象限.随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=mx-1(m<0)上运动,则m与k的关系是( )

A. m= -kB. m=![]() kC. m= -2kD. m= -3k
kC. m= -2kD. m= -3k
查看答案和解析>>
科目: 来源: 题型:
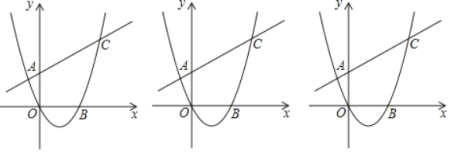
【题目】如图,二次函数y=ax2﹣4ax(a≠0)的图象与直线y=kx+3交于点A(﹣1,![]() )、点C两点.
)、点C两点.
(1)求a,k的值;
(2)点P在第一象限的抛物线上,其横坐标为t,连接PC、PA,设△PCA的面积为S,求S关于t的函数关系式:(直接写出t的取值范围)
(3)在(2)的条件下,作CE⊥x轴于E,点P直线y=kx+3下方时,连接OP、BC交于D,连接ED,当∠ODE=90°时,求t和S的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com