
科目: 来源: 题型:
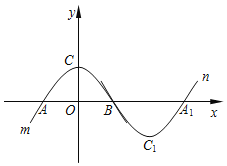
【题目】如图所示,抛物线m:![]() 与x轴于点A、
与x轴于点A、![]() 点A在点B的左侧
点A在点B的左侧![]() ,与y轴交于点
,与y轴交于点![]() 将抛物线m绕点B旋转
将抛物线m绕点B旋转![]() ,得到新的抛物线n,它的顶点为
,得到新的抛物线n,它的顶点为![]() ,与x轴的另一个交点为
,与x轴的另一个交点为![]() .
.
![]() 当
当![]() ,
,![]() 时,求抛物线n的解析式;
时,求抛物线n的解析式;
![]() 求证:四边形
求证:四边形![]() 是平行四边形;
是平行四边形;
![]() 当
当![]() 时,四边形
时,四边形![]() 可能是矩形吗?若能,请求出抛物线m的解析式;若不能,请说明理由.
可能是矩形吗?若能,请求出抛物线m的解析式;若不能,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】对任意一个正整数m,如果![]() ,其中n是正整数,则称m为“优数”,n为m的最优拆分点,例如:
,其中n是正整数,则称m为“优数”,n为m的最优拆分点,例如:![]() ,则72是一个“优数”,8为72的最优拆分点.
,则72是一个“优数”,8为72的最优拆分点.
![]() 请写出一个大于40小于50的“优数”______,它的最优拆分点是______.
请写出一个大于40小于50的“优数”______,它的最优拆分点是______.
![]() 把“优数”p的2倍与“优数”q的3倍的差记为
把“优数”p的2倍与“优数”q的3倍的差记为![]() ,例如:
,例如:![]() ,
,![]() ,则
,则![]() 若“优数”p的最优拆分点为
若“优数”p的最优拆分点为![]() ,“优数”q的最优拆分点为t,当
,“优数”q的最优拆分点为t,当![]() 时,求t的值并判断它是否为“优数”.
时,求t的值并判断它是否为“优数”.
查看答案和解析>>
科目: 来源: 题型:
【题目】綦江中学新校区建设正按计划顺利推进,其中有一块矩形地面准备用同样规格的黑、白两色的正方形瓷砖按如图所示的设计进行铺设,请观察下列图形并解答有关问题.
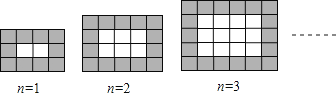
![]() 第n个图中共有块瓷砖
第n个图中共有块瓷砖![]() 用含n的代数式表示
用含n的代数式表示![]() ;
;
![]() 按上述铺设方案,铺这块矩形地面共用了506块瓷砖,求此时n的值;
按上述铺设方案,铺这块矩形地面共用了506块瓷砖,求此时n的值;
![]() 是否存在黑瓷砖与白瓷砖块数相等的情形?请通过计算说明理由.
是否存在黑瓷砖与白瓷砖块数相等的情形?请通过计算说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】善于不断改进学习方法的小迪发现,对解题进行回顾反思,学习效果更好.某一天小迪有20分钟时间可用于学习.假设小迪用于解题的时间![]() (单位:分钟)与学习收益量
(单位:分钟)与学习收益量![]() 的关系如图1所示,用于回顾反思的时间
的关系如图1所示,用于回顾反思的时间![]() (单位:分钟)与学习收益
(单位:分钟)与学习收益![]() 的关系如图2所示(其中
的关系如图2所示(其中![]() 是抛物线的一部分,
是抛物线的一部分,![]() 为抛物线的顶点),且用于回顾反思的时间不超过用于解题的时间.
为抛物线的顶点),且用于回顾反思的时间不超过用于解题的时间.
(1)求小迪解题的学习收益量![]() 与用于解题的时间
与用于解题的时间![]() 之间的函数关系式;
之间的函数关系式;
(2)求小迪回顾反思的学习收益量![]() 与用于回顾反思的时间
与用于回顾反思的时间![]() 的函数关系式;
的函数关系式;
(3)问小迪如何分配解题和回顾反思的时间,才能使这20分钟的学习收益总量最大?
查看答案和解析>>
科目: 来源: 题型:
【题目】已知Rt△ABC中,∠ACB=90°,CA=CB=4,另有一块等腰直角三角板的直角顶点放在C处,CP=CQ=2,将三角板CPQ绕点C旋转(保持点P在△ABC内部),连接AP、BP、BQ.
(1)如图1求证:AP=BQ;
(2)如图2当三角板CPQ绕点C旋转到点A、P、Q在同一直线时,求AP的长;
(3)设射线AP与射线BQ相交于点E,连接EC,写出旋转过程中EP、EQ、EC之间的数量关系.

查看答案和解析>>
科目: 来源: 题型:
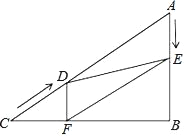
【题目】如图,在Rt△ABC中,∠B=90°,AC=40cm,∠A=60°,点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(0<t≤10),过点D作DF⊥BC于点F,连接DE,EF.
(1)四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,请说明理由;
(2)当t为何值时,△DEF为直角三角形?请说明理由.
查看答案和解析>>
科目: 来源: 题型:
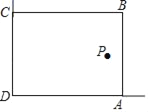
【题目】在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用32m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=xm.
(1)若花园的面积为252m2,求x的值;
(2)若在P处有一棵树与墙CD,AD的距离分别是17m和6m,要将这棵树围在花园内(含边界,不考虑树的粗细),求花园面积S的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某校在宣传“民族团结”活动中,采用四种宣传形式:A.器乐,B.舞蹈,C.朗诵,D.唱歌.每名学生从中选择并且只能选择一种最喜欢的,学校就宣传形式对学生进行了抽样调查,并将调查结果绘制了如下两幅不完整的统计图.

请结合图中所给信息,解答下列问题:
(1)本次调查的学生共有_____人;
(2)补全条形统计图;
(3)该校共有1200名学生,请估计选择“唱歌”的学生有多少人?
(4)七年一班在最喜欢“器乐”的学生中,有甲、乙、丙、丁四位同学表现优秀,现从这四位同学中随机选出两名同学参加学校的器乐队,请用列表或画树状图法求被选取的两人恰好是甲和乙的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与反比例函数y=![]() 的图象交于A、B两点.
的图象交于A、B两点.
(1)利用图中的条件,求反比例函数和一次函数的解析式.
(2)求△AOB的面积.
(3)根据图象直接写出使一次函数的值大于反比例函数的值的x的取值范围.

查看答案和解析>>
科目: 来源: 题型:
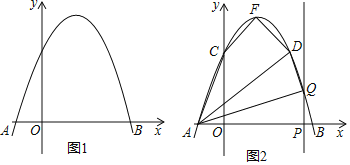
【题目】如图1,抛物线y=ax2+bx+3交x轴于点A(﹣1,0)和点B(3,0).
(1)求该抛物线所对应的函数解析式;
(2)如图2,该抛物线与y轴交于点C,顶点为F,点D(2,3)在该抛物线上.
①求四边形ACFD的面积;
②点P是线段AB上的动点(点P不与点A、B重合),过点P作PQ⊥x轴交该抛物线于点Q,连接AQ、DQ,当△AQD是直角三角形时,求出所有满足条件的点Q的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com