
科目: 来源: 题型:
【题目】《山西省新能源汽车产业2018年行动计划》指出,2018年全省新能源汽车产能将达到30万辆,按照“十三五”规划,到2020年,全省新能源汽车产能将达到41万辆,若设这两年全省新能源汽车产能的平均增长率为![]() ,则根据题意可列出方程是()
,则根据题意可列出方程是()
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
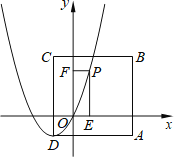
【题目】如图,在正方形ABCD中,点A的坐标为(![]() ,
,![]() ),点D的坐标为(
),点D的坐标为(![]() ,
,![]() ),且AB∥y轴,AD∥x轴. 点P是抛物线
),且AB∥y轴,AD∥x轴. 点P是抛物线![]() 上一点,过点P作PE⊥x轴于点E,PF⊥y轴于点 F.
上一点,过点P作PE⊥x轴于点E,PF⊥y轴于点 F.
(1)直接写出点![]() 的坐标;
的坐标;
(2)若点P在第二象限,当四边形PEOF是正方形时,求正方形PEOF的边长;
(3)以点E为顶点的抛物线![]() 经过点F,当点P在正方形ABCD内部(不包含边)时,求a的取值范围.
经过点F,当点P在正方形ABCD内部(不包含边)时,求a的取值范围.
查看答案和解析>>
科目: 来源: 题型:
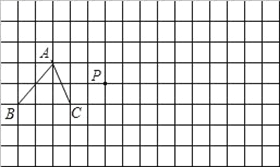
【题目】在下面16×8的正方形网格中,每个小正方形的边长为1个单位,△ABC是格点三角形(顶点在网格交点处),请你画出:
(1)△ABC的中心对称图形,A点为对称中心;
(2)△ABC关于点P的位似△A′B′C′,且位似比为1:2;
(3)以A、B、C、D为顶点的所有格点平行四边形ABCD的顶点D.
查看答案和解析>>
科目: 来源: 题型:
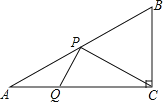
【题目】在Rt△ABC中,∠BAC=30°,斜边AB=2![]() ,动点P在AB边上,动点Q在AC边上,且∠CPQ=90°,则线段CQ长的最小值=__________ .
,动点P在AB边上,动点Q在AC边上,且∠CPQ=90°,则线段CQ长的最小值=__________ .
查看答案和解析>>
科目: 来源: 题型:
【题目】(12分)阅读理解:
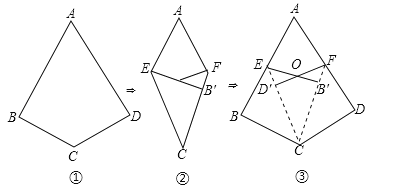
如图①,如果四边形ABCD满足AB=AD,CB=CD,∠B=∠D=90°,那么我们把这样的四边形叫做“完美筝形”.
将一张如图①所示的“完美筝形”纸片ABCD先折叠成如图②所示形状,再展开得到图③,其中CE,CF为折痕,∠BCE=∠ECF=∠FCD,点B′为点B的对应点,点D′为点D的对应点,连接EB′,FD′相交于点O.
简单应用:
(1)在平行四边形、矩形、菱形、正方形四种图形中,一定为“完美筝形”的是 ;
(2)当图③中的∠BCD=120°时,∠AEB′= °;
(3)当图②中的四边形AECF为菱形时,对应图③中的“完美筝形”有 个(包含四边形ABCD).
拓展提升:
(4)当图③中的∠BCD=90°时,连接AB′,请探求∠AB′E的度数,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】为了了解学生关注热点新闻的情况,“两会”期间,小明对班级同学一周内收看“两会”新闻的次数情况作了调查,调查结果统计如图所示(其中男生收看![]() 次的人数没有标出).
次的人数没有标出).
根据上述信息,解答下列各题:
 ×
×
(1)该班级女生人数是__________,女生收看“两会”新闻次数的中位数是________;
(2)对于某个群体,我们把一周内收看某热点新闻次数不低于![]() 次的人数占其所在群体总人数的百分比叫做该群体对某热点新闻的“关注指数”.如果该班级男生对“两会”新闻的“关注指数”比女生低
次的人数占其所在群体总人数的百分比叫做该群体对某热点新闻的“关注指数”.如果该班级男生对“两会”新闻的“关注指数”比女生低![]() ,试求该班级男生人数;
,试求该班级男生人数;
(3)为进一步分析该班级男、女生收看“两会”新闻次数的特点,小明给出了男生的部分统计量(如表).
统计量 | 平均数(次) | 中位数(次) | 众数(次) | 方差 | … |
该班级男生 |
|
|
|
| … |
根据你所学过的统计知识,适当计算女生的有关统计量,进而比较该班级男、女生收看“两会”新闻次数的波动大小.
查看答案和解析>>
科目: 来源: 题型:
【题目】现在,苏宁商场进行促销活动,出售一种优惠购物卡(注:此卡只作为购物优惠凭证不能顶替货款),花300元买这种卡后,凭卡可在这家商场按标价的8折购物.
(1)顾客购买多少元金额的商品时,买卡与不买卡花钱相等?在什么情况下购物合算?
(2)小张要买一台标价为3500元的冰箱,如何购买合算?小张能节省多少元钱?
(3)小张按合算的方案,把这台冰箱买下,如果商场还能盈利25%,这台冰箱的进价是多少元?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,点![]() ,
, ![]() 在反比例函数
在反比例函数![]() (m为常数)的图象上,连接AO并延长与图象的另一支有另一个交点为点C,过点A的直线l与x轴的交点为点
(m为常数)的图象上,连接AO并延长与图象的另一支有另一个交点为点C,过点A的直线l与x轴的交点为点![]() ,过点C作CE∥x轴交直线l于点E.
,过点C作CE∥x轴交直线l于点E.
(1)求m的值,并求直线l对应的函数解析式;
(2)求点E的坐标;
(3)过点B作射线BN∥x轴,与AE交于点M (补全图形),求证: ![]()
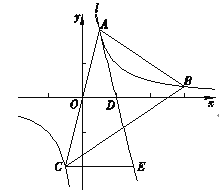
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,点P的坐标为(0,4),直线y=![]() x-3与x轴、y轴分别交于点A、B,点M是直线AB上的一个动点,则PM的最小值为________.
x-3与x轴、y轴分别交于点A、B,点M是直线AB上的一个动点,则PM的最小值为________.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,△ABC中,∠B=90°,AB=6cm,BC=8cm.
(1)点P从点A开始沿AB边向B以1cm/s的速度移动,点Q从B点开始沿BC边向点C以2cm/s的速度移动.如果P,Q分别从A,B同时出发,经过几秒,使△PBQ的面积等于8cm2?
(2)点P从点A开始沿AB边向B以1cm/s的速度移动,点Q从B点开始沿BC边向点C以2cm/s的速度移动.如果P,Q分别从A,B同时出发,线段PQ能否将△ABC分成面积相等的两部分?若能,求出运动时间;若不能说明理由.
(3)若P点沿射线AB方向从A点出发以1cm/s的速度移动,点Q沿射线CB方向从C点出发以2cm/s的速度移动,P,Q同时出发,问几秒后,△PBQ的面积为1?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com