
科目: 来源: 题型:
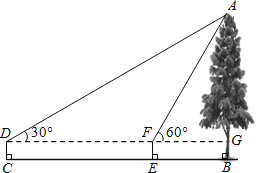
【题目】如图,小红同学用仪器测量一棵大树AB的高度,在C处测得∠ADG=30°,在E处测得∠AFG=60°,CE=8米,仪器高度CD=1.5米,求这棵树AB的高度(结果保留两位有效数字,![]() ≈1.732).
≈1.732).
查看答案和解析>>
科目: 来源: 题型:
【题目】某商场为了吸引顾客,设计了一种促销活动.在一个不透明的箱子里放有4个完全相同的小球,球上分别标有“0元”、“10元”、“30元”和“50元”的字样.规定:顾客在本商场同一日内,消费每满300元,就可以从箱子里先后摸出两个球(每次只摸出一个球,第一次摸出后不放回).商场根据两个小球所标金额之和返还相应价格的购物券,可以重新在本商场消费.某顾客消费刚好满300元,则在本次消费中:
(1)该顾客至少可得___元购物券,至多可得___元购物券;
(2)请用画树状图或列表法,求出该顾客所获购物券的金额不低于50元的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】某商品的进价为每件40元,售价为每件50元,每个月可卖出200件![]() 如每件商品的售价每上涨1元,则每个月少卖5件
如每件商品的售价每上涨1元,则每个月少卖5件![]() 设每件商品的售价上涨x元,每个月销售利润为y元.
设每件商品的售价上涨x元,每个月销售利润为y元.
![]() 求y与x的函数关系式;
求y与x的函数关系式;
![]() 每件商品的售价定为多少元时,每个月可获得最大利润?最大的月利润是多少元?
每件商品的售价定为多少元时,每个月可获得最大利润?最大的月利润是多少元?
![]() 每件商品的售价定在什么范围时,每个月的利润不低于3000元?
每件商品的售价定在什么范围时,每个月的利润不低于3000元?
查看答案和解析>>
科目: 来源: 题型:
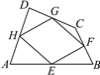
【题目】如图,顺次连接四边形ABCD各边的中点得到四边形EFGH,要使四边形EFGH为菱形,应添加的条件是( )
A. AB∥DC B. AB=DC
C. AC⊥BD D. AC=BD
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知一次函数![]() 的图象分别与x轴、y轴交于点A、C,与反比列函数
的图象分别与x轴、y轴交于点A、C,与反比列函数![]() 的图象在第一象限内交于点P,过点P作
的图象在第一象限内交于点P,过点P作![]() 轴,垂足为B,且
轴,垂足为B,且![]() 的面积为9.
的面积为9.

![]() 点A的坐标为______,点C的坐标为______,点P的坐标为______;
点A的坐标为______,点C的坐标为______,点P的坐标为______;
![]() 已知点Q在反比例函数
已知点Q在反比例函数![]() 的图象上,其横坐标为6,在x轴上确定一点M,使得
的图象上,其横坐标为6,在x轴上确定一点M,使得![]() 的周长最小,求出点M的坐标;
的周长最小,求出点M的坐标;
![]() 设点E是反比例函数
设点E是反比例函数![]() 在第一象限内图象上的一动点,且点E在直线PB的右侧,过点E作
在第一象限内图象上的一动点,且点E在直线PB的右侧,过点E作![]() 轴,垂足为F,当
轴,垂足为F,当![]() 和
和![]() 相似时,求动点E的坐标.
相似时,求动点E的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】小明与同学们在数学动手实践操作活动中,将锐角为![]() 的直角三角板MPN的一个锐角顶点P与正方形ABCD的顶点A重合,正方形ABCD固定不动,然后将三角板绕着点A旋转,
的直角三角板MPN的一个锐角顶点P与正方形ABCD的顶点A重合,正方形ABCD固定不动,然后将三角板绕着点A旋转,![]() 的两边分别与正方形的边BC、DC或其延长线相交于点E、F,连结EF.
的两边分别与正方形的边BC、DC或其延长线相交于点E、F,连结EF.
(探究发现)
![]() 在三角板旋转过程中,当
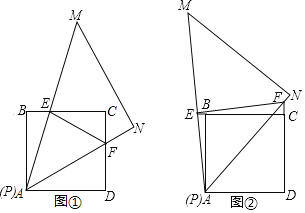
在三角板旋转过程中,当![]() 的两边分别与正方形的边CB、DC相交时,如图
的两边分别与正方形的边CB、DC相交时,如图![]() 所示,请直接写出线段BE、DF、EF满足的数量关系:______.
所示,请直接写出线段BE、DF、EF满足的数量关系:______.
(拓展思考)
![]() 在三角板旋转过程中,当
在三角板旋转过程中,当![]() 的两边分别与正方形的边CB、DC的延长线相交时,如图
的两边分别与正方形的边CB、DC的延长线相交时,如图![]() 所示,则线段BE、DF、EF又将满足怎样的数量关系:______,并证明你的结论;
所示,则线段BE、DF、EF又将满足怎样的数量关系:______,并证明你的结论;
(创新应用)
![]() 若正方形的边长为4,在三角板旋转过程中,当
若正方形的边长为4,在三角板旋转过程中,当![]() 的一边恰好经过BC边的中点时,试求线段EF的长.
的一边恰好经过BC边的中点时,试求线段EF的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】某市著名景点“凤凰楼”,一耸入云的文化丰碑,坐落于凤凰山之巅![]() 周末,阳光明媚,小明、小芳等同学一起登凤凰山,在山顶,他们想用一些测量工具和所学知识测量“凤凰楼”的高度来检验自己掌握知识和运用知识的能力
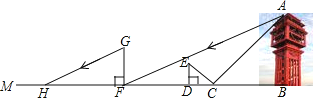
周末,阳光明媚,小明、小芳等同学一起登凤凰山,在山顶,他们想用一些测量工具和所学知识测量“凤凰楼”的高度来检验自己掌握知识和运用知识的能力![]() 他们经过观察发现,观测点与“凤凰楼”底部间的距离不易测得,因此他们运用如下方法来进行测量:如图,小芳在小明和“凤凰楼”之间的直线BM上放一平面镜,在镜面上做一个标记,这个标记在直线BM上对应位置为点C,镜子不动,小明看着镜面上的标记,他来回走动,走到点D时,看到“凤凰楼”顶端点A在镜面中的像与镜面上的标记重合,这时,测得小明眼睛与地面的高度
他们经过观察发现,观测点与“凤凰楼”底部间的距离不易测得,因此他们运用如下方法来进行测量:如图,小芳在小明和“凤凰楼”之间的直线BM上放一平面镜,在镜面上做一个标记,这个标记在直线BM上对应位置为点C,镜子不动,小明看着镜面上的标记,他来回走动,走到点D时,看到“凤凰楼”顶端点A在镜面中的像与镜面上的标记重合,这时,测得小明眼睛与地面的高度![]() 米,
米,![]() 米,然后,小明从点D沿DM方向走了24米,到达“凤凰楼”影子的末端F处,此时,测的小明身高FG的影长
米,然后,小明从点D沿DM方向走了24米,到达“凤凰楼”影子的末端F处,此时,测的小明身高FG的影长![]() 米,
米,![]() 米
米![]() 如图,已知
如图,已知![]() ,
,![]() ,
,![]() ,其中,测量时所使用的平面镜厚度忽略不计
,其中,测量时所使用的平面镜厚度忽略不计![]() 请你根据题中提供的相关信息,求出“凤凰楼”的高AB的长度.
请你根据题中提供的相关信息,求出“凤凰楼”的高AB的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com