
科目: 来源: 题型:
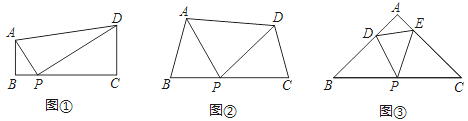
【题目】感知:如图①,在四边形ABCD中,AB∥CD,∠B=90°,点P在BC边上,当∠APD=90°时,可知△ABP∽△PCD.(不要求证明)
探究:如图②,在四边形ABCD中,点P在BC边上,当∠B=∠C=∠APD时,求证:△ABP∽△PCD.
拓展:如图③,在△ABC中,点P是边BC的中点,点D、E分别在边AB、AC上.若∠B=∠C=∠DPE=45°,BC=6![]() ,CE=4,则DE的长为 .
,CE=4,则DE的长为 .
查看答案和解析>>
科目: 来源: 题型:
【题目】襄阳市精准扶贫工作已进入攻坚阶段.贫困户张大爷在某单位的帮扶下,把一片坡地改造后种植了优质水果蓝莓,今年正式上市销售.在销售的30天中,第一天卖出20千克,为了扩大销量,采取了降价措施,以后每天比前一天多卖出4千克.第x天的售价为y元/千克,y关于x的函数解析式为![]() 且第12天的售价为32元/千克,第26天的售价为25元/千克.已知种植销售蓝莓的成木是18元/千克,每天的利润是W元(利润=销售收入﹣成本).
且第12天的售价为32元/千克,第26天的售价为25元/千克.已知种植销售蓝莓的成木是18元/千克,每天的利润是W元(利润=销售收入﹣成本).
(1)m= ,n= ;
(2)求销售蓝莓第几天时,当天的利润最大?最大利润是多少?
(3)在销售蓝莓的30天中,当天利润不低于870元的共有多少天?
查看答案和解析>>
科目: 来源: 题型:
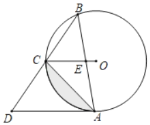
【题目】如图,已知⊙O是△ABC的外接圆,连接OC,过点A作AD∥OC,交BC的延长线于D,AB交OC于E,∠ABC=45°.
(1)求证:AD是⊙O的切线;
(2)若AE=![]() ,CE=3.
,CE=3.
①求⊙O的半径;
②求图中阴影部分的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
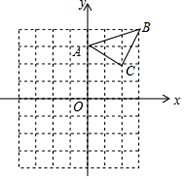
(1)△ABC向下平移4个单位长度得到的△A1B1C1,点C1的坐标是 ;
(2)以点B为位似中心,在网格内画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2:1,点C2的坐标是 ;(画出图形)
(3)△A2B2C2的面积是 平方单位.
查看答案和解析>>
科目: 来源: 题型:
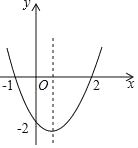
【题目】二次函数y=ax2+bx+c的图象如图所示,以下结论:①abc>0;②4ac<b2;③2a+b>0;④其顶点坐标为(![]() ,﹣2);⑤当x<
,﹣2);⑤当x<![]() 时,y随x的增大而减小;⑥a+b+c>0;⑦方程ax2+bx+c=﹣4有实数解,正确的有( )
时,y随x的增大而减小;⑥a+b+c>0;⑦方程ax2+bx+c=﹣4有实数解,正确的有( )
A. 3个 B. 4个 C. 5个 D. 6个
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知等边△ABC的边长为8,以AB为直径的圆交BC于点F.以C为圆心,CF长为半径作图,D是⊙C上一动点,E为BD的中点,当AE最大时,BD的长为( )

A. ![]() B.
B. ![]() C.
C. ![]() D. 12
D. 12
查看答案和解析>>
科目: 来源: 题型:
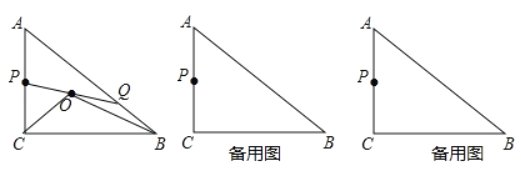
【题目】已知,如图Rt△ABC中,∠C=90°,AC=6cm,BC=8cm,点P为AC的中点,Q从点A运动到B,点Q运动到点B停止,连接PQ,取PQ的中点O,连接OC,OB.
(1)若△ABC∽△APQ,求BQ的长;
(2)在整个运动过程中,点O的运动路径长_____;
(3)以O为圆心,OQ长为半径作⊙O,当⊙O与AB相切时,求△COB的面积.
查看答案和解析>>
科目: 来源: 题型:
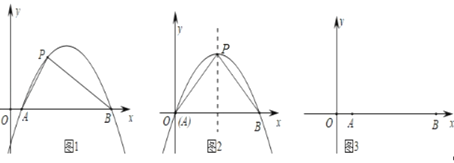
【题目】如图1,抛物线y=ax2+bx+c(a≠0)与x轴交于A,B两点,点P在抛物线上(与A,B两点不重合),若△ABP的三边满足AP2+BP2=AB2,则我们称点P为抛物线y=ax2+bx+c(a≠0)的勾股点.
(1)直接写出抛物线y=x2﹣1的勾股点坐标为_____;
(2)如图2,已知抛物线:y=ax2+bx(a<0,b>0)与x轴交于A、B两点,点P为抛物线的顶点,问点P能否为抛物线的勾股点,若能,求出b的值;
(3)如图3,在平面直角坐标系中,点A(2,0),B(12,0),点P到x轴的距离为1,点P是过A、B两点的抛物线上的勾股点,求过P、A、B三点的抛物线的解析式和点P的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】“春节”前夕,某超市购进某种品牌礼品,每盒进价是40元,超市规定每盒售价不得少于45元,设每盒售价为x(元),每天的销售量y(盒),y与x成一次的函数关系,经过市场调查获得部分数据如下表:
每盒售价为x(元) | 45 | 50 | 55 | … |
每天的销售量y(盒) | 450 | 400 | 350 | … |
(1)试求出y与x之间的函数关系式;
(2)当每盒售价定为多少元时,每天销售的利润P(元)最大?最大利润是多少?
(3)物价部门规定:这种礼品每盒售价不得高于60元,如果超市想要每天获得不低于5250元的利润,那么超市每天至少销售这种礼品多少盒?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com