
科目: 来源: 题型:
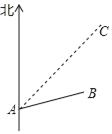
【题目】如图,台风中心位于点A,并沿东北方向AC移动,已知台风移动的速度为50千米/时,受影响区域的半径为130千米,B市位于点A的北偏东75°方向上,距离A点240千米处.
(1)说明本次台风会影响B市;
(2)求这次台风影响B市的时间.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知y关于x二次函数y=x2﹣(2k+1)x+(k2+5k+9)与x轴有交点.
(1)求k的取值范围;
(2)若x1,x2是关于x的方程x2﹣(2k+1)x+(k2+5k+9)=0的两个实数根,且x12+x22=39,求k的值.
查看答案和解析>>
科目: 来源: 题型:
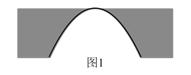
【题目】河上有一座桥孔为抛物线形的拱桥(如图 ![]() ),水面宽
),水面宽 ![]() 时,水面离桥孔顶部
时,水面离桥孔顶部 ![]() ,因降暴雨水面上升
,因降暴雨水面上升 ![]() .
.
(1)建立适当的坐标系,并求暴雨后水面的宽;(结果保留根号)
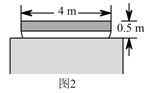
(2)一艘装满物资的小船,露出水面的部分高为 ![]() ,宽
,宽 ![]() (横断面如图
(横断面如图 ![]() 所示),暴雨后这艘船能从这座拱桥下通过吗?
所示),暴雨后这艘船能从这座拱桥下通过吗?
查看答案和解析>>
科目: 来源: 题型:
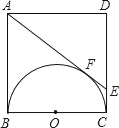
【题目】如图,正方形ABCD的边长为4cm,以正方形的一边BC为直径在正方形ABCD内作半圆,再过点A作半圆的切线,与半圆切于点F,与CD交于点E,则S梯形ABCE=_____cm2.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+c的图象经过点(0,3),(x1,0),其中,2<x1<3,对称轴为x=1,则下列结论:①2a﹣b=0; ②x(ax+b)≤a+b;③方程ax2+bx+c﹣3=0的两根为x1'=0,x2'=2;④﹣3<a<﹣1.其中正确的是( )
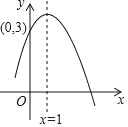
A. ②③④B. ①②③C. ②④D. ②③
查看答案和解析>>
科目: 来源: 题型:
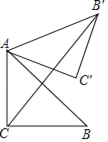
【题目】如图,在△ABC中,∠ACB=90°,AC=BC=![]() ,将△ACB绕点A逆时针旋转60°得到△AC′B′,则CB′的长为( )
,将△ACB绕点A逆时针旋转60°得到△AC′B′,则CB′的长为( )
A. ![]() +
+![]() B. 1+
B. 1+![]() C. 3D.
C. 3D. ![]() +
+![]()
查看答案和解析>>
科目: 来源: 题型:
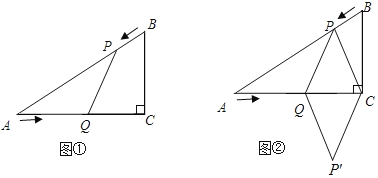
【题目】已知:如图①,在Rt△ABC中,∠C=90°,AC=8cm,BC=6cm,点P由B出发沿BA方向向点A匀速运动,速度为1cm/s;点Q由A出发沿AC方向向点C匀速运动,速度为2cm/s;连接PQ.若设运动的时间为t(s)(0<t<4),解答下列问题:
(1)当t为何值时,PQ∥BC;
(2)设△AQP的面积为y(cm2),求y与t之间的函数关系式;
(3)是否存在某一时刻t,使线段PQ恰好把Rt△ACB的周长和面积同时平分?若存在,求出此时t的值;若不存在,说明理由;
(4)如图②,连接PC,并把△PQC沿QC翻折,得到四边形PQP′C,那么是否存在某一时刻t,使四边形PQP′C为菱形?若存在,求出此时菱形的边长;若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】问题提出:
有n个环环相扣的圆环形成一串线型链条,当只断开其中的k(k<n)个环,要求第一次取走一个环,以后每次都只能比前一次多得一个环,则最多能得到的环数n是多少呢?
问题探究:
为了找出n与k之间的关系,我们运用一般问题特殊化的方法,从特殊到一般,归纳出解决问题的方法.
探究一:k=1,即断开链条其中的1个环,最多能得到几个环呢?
当n=1,2,3时,断开任何一个环,都能满足要求,分次取走;
当n=4时,断开第二个环,如图①,第一次取走1环;第二次退回1环换取2环,得2个环;第三次再取回1环,得3个环;第四次再取另1环,得4个环,按要求分4次取走.
当n=5,6,7时,如图②,图③,图④方式断开,可以用类似上面的方法,按要求分5,6,7次取走.
当n=8时,如图⑤,无论断开哪个环,都不可能按要求分次取走.
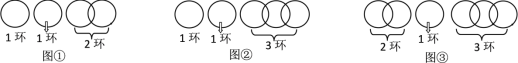
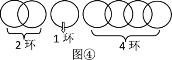
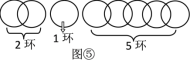
所以,当断开1个环时,从得到更多环数的角度考虑,把链条分成3部分,分别是1环、2环和4环,最多能得到7个环.
即当k=1时,最多能得到的环数n=1+2+4=1+2×3=1+2×(22-1)=7.
探究二:k=2,即断开链条其中的2个环,最多能得到几个环呢?
从得到更多环数的角度考虑,按图⑥方式断开,把链条分成5部分,按照类似探究一的方法,按要求分1,2,…23次取走.
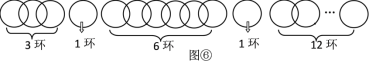
所以,当断开2个环时,把链条分成5部分,分别是1环、1环、3环、6环、12环,最多能得到23个环.
即当k=2时,最多能得到的环数n=1+1+3+6+12=2+3×7=2+3×(23-1)=23.
探究三:k=3,即断开链条其中的3个环,最多能得到几个环呢?
从得到更多环数的角度考虑,按图⑦方式断开,把链条分成7部分,按照类似前面探究的方法,按要求分1,2,…63次取走.
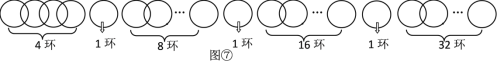
所以,当断开3个环时,从得到更多环数的角度考虑,把链条分成7部分,分别是1环、1环、1环、4环、8环、16环、32环,最多能得到63个环.
即当k=3时,最多能得到的环数n=1+1+1+4+8+16+32=3+4×15=3+4×(24-1)=63.
探究四:k=4,即断开链条其中的4个环,最多能得到几个环呢?
按照类似前面探究的方法,当断开4个环时,从得到更多环数的角度考虑,把链条分成 部分,分别为 ,最多能得到的环数n= .请画出如图⑥的示意图.
模型建立:
有n个环环相扣的圆环形成一串线型链条,断开其中的k(k<n)个环,从得到更多环数的角度考虑,把链条分成 部分,
分别是:1、1、1……1、k+1、 、……、 ,最多能得到的环数n = .
实际应用:
一天一位财主对雇工说:“你给我做两年的工,我每天付给你一个银环.不过,我用一串环环相扣的线型银链付你工钱,但你最多只能断开银链中的6个环.如果你无法做到每天取走一个环,那么你就得不到这两年的工钱,如果银链还有剩余,全部归你!你愿意吗?”
聪明的你是否可以运用本题的方法通过计算帮助雇工解决这个难题,雇工最多能得到总环数为多少环的银链?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,ABCD的对角线AC、BD相交于点O,OE=OF.
(1)求证:△BOE≌△DOF;
(2)若BD=EF,连接DE、BF,判断四边形EBFD的形状,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com