
科目: 来源: 题型:
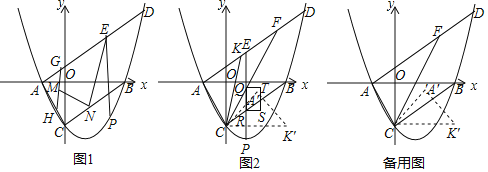
【题目】如图,抛物线y=![]() 与x轴交于A,B(点A在点B的左侧)与y轴交于点C,连接AC、BC.过点A作AD∥BC交抛物线于点D(8
与x轴交于A,B(点A在点B的左侧)与y轴交于点C,连接AC、BC.过点A作AD∥BC交抛物线于点D(8![]() ,10),点P为线段BC下方抛物线上的任意一点,过点P作PE∥y轴交线段AD于点E.
,10),点P为线段BC下方抛物线上的任意一点,过点P作PE∥y轴交线段AD于点E.
(1)如图1.当PE+AE最大时,分别取线段AE,AC上动点G,H,使GH=5,若点M为GH的中点,点N为线段CB上一动点,连接EN、MN,求EN+MN的最小值;
(2)如图2,点F在线段AD上,且AF:DF=7:3,连接CF,点Q,R分别是PE与线段CF,BC的交点,以RQ为边,在RQ的右侧作矩形RQTS,其中RS=2,作∠ACB的角平分线CK交AD于点K,将△ACK绕点C顺时针旋转75°得到△A′CK′,当矩形RQTS与△A′CK′重叠部分(面积不为0)为轴对称图形时,请直接写出点P横坐标的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】“构造图形解题”,它的应用十分广泛,特别是有些技巧性很强的题目,如果不能发现题目中所隐含的几何意义,而用通常的代数方法去思考,经常让我们手足无措,难以下手,这时,如果能转换思维,发现题目中隐含的几何条件,通过构造适合的几何图形,将会得到事半功倍的效果,下面介绍两则实例:
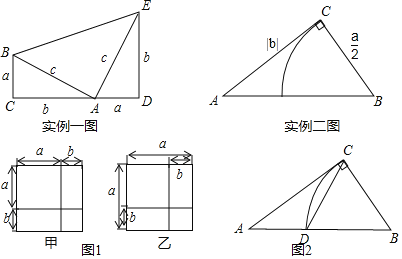
实例一:1876年,美国总统伽非尔德利用实例一图证明了勾股定理:由S四边形ABCD=S△ABC+S△ADE+S△ABE得:![]() (a+b)2=2×
(a+b)2=2×![]() ab+
ab+![]() c2,化简得:a2+b2=c2.
c2,化简得:a2+b2=c2.
实例二:欧几里得的《几何原本》记载,关于x的方程x2+ax=b2的图解法是:画Rt△ABC,使∠ACB=90°,BC=![]() ,AC=|b|,再在斜边AB上截取BD=
,AC=|b|,再在斜边AB上截取BD=![]() ,则AD的长就是该方程的一个正根(如实例二图).
,则AD的长就是该方程的一个正根(如实例二图).
请根据以上阅读材料回答下面的问题:
(1)如图1,请利用图形中面积的等量关系,写出甲图要证明的数学公式是______,乙图要证明的数学公式是______,体现的数学思想是______;
(2)如图2,若2和-8是关于x的方程x2+ax=b2的两个根,按照实例二的方式构造Rt△ABC,连接CD,求CD的长;
(3)若x,y,z都为正数,且x2+y2=z2,请用构造图形的方法求![]() 的最大值.
的最大值.
查看答案和解析>>
科目: 来源: 题型:
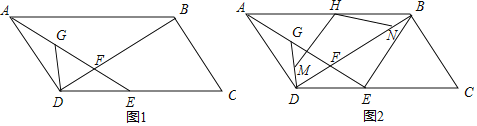
【题目】如图,在平行四边形ABCD中,对角线BD⊥AD,E为CD上一点,连接AE交BD于点F,G为AF的中点,连接DG.
(1)如图1,若DG=DF=1,BF=3,求CD的长;
(2)如图2,连接BE,且BE=AD,∠AEB=90°,M、N分别为DG,BD上的点,且DM=BN,H为AB的中点,连接HM、HN,求证:∠MHN=∠AFB.
查看答案和解析>>
科目: 来源: 题型:
【题目】随着经济水平的不断提升,越来越多的人选择到电影院去观看电影,体验视觉盛宴,并且更多的人通过淘票票,猫眼等网上平台购票,快捷且享受更多优惠,电影票价格也越来越便宜.2018年从网上平台购买5张电影票的费用比在现场购买3张电影票的费用少10元,从网上平台购买4张电影票的费用和现场购买2张电影票的费用共为190元.
(1)请问2018年在网上平台购票和现场购票的每张电影票的价格各为多少元?
(2)2019年“元旦”当天,南坪上海城的“华谊兄弟影院”按照2018年在网上平台购票和现场购票的电影票的价格进行销售,当天网上和现场售出电影票总票数为600张.“元旦”假期刚过,观影人数出现下降,于是该影院决定将1月2日的现场购票的价格下调,网上购票价格保持不变,结果发现现场购票每张电影票的价格每降价0.5元,则当天总票数比“元旦”当天总票数增加4张,经统计,1月2日的总票数中有![]() 通过网上平台售出,其余均由电影院现场售出,且当天票房总收益为19800元,请问该电影院在1月2日当天现场购票每张电影票的价格下调了多少元?
通过网上平台售出,其余均由电影院现场售出,且当天票房总收益为19800元,请问该电影院在1月2日当天现场购票每张电影票的价格下调了多少元?
查看答案和解析>>
科目: 来源: 题型:
【题目】初三某班同学小戴想根据学习函数的经验,通过研究一个未学过的函数的图象,从而探究其各方面性质.
下表是函数y与自变量x的几组对应值:
x | … | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 9 | 12 | … |
y | … | -4 | 0 | 4 | 8 | 12 | 9 | 7.2 | 6 | 4 | 3 | … |
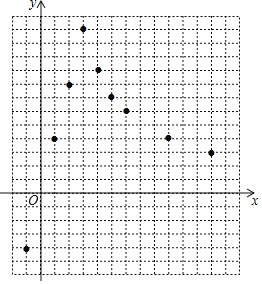
(1)在平面直角坐标系xOy中,每个小正方形的边长为一个单位长度,描出了以上表中各对对应值为坐标的点,请根据描出的点,画出该函数的图象.
(2)请根据画出的函数图象,直接写出该函数的关系式y=______(请写出自变量的取值范围),并写出该函数的一条性质:______.
(3)当直线y=-![]() x+b与该函数图象有3个交点时,求b的取值范围.
x+b与该函数图象有3个交点时,求b的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】“学而时习之,不亦乐乎!”,古人把经常复习当作是一种乐趣,能达到这种境界是非常不容易的.复习可以让遗忘的知识得到补拾,零散的知识变得系统,薄弱的知识有所强化,掌握的知识更加巩固,生疏的技能得到训练.为了了解初一学生每周的复习情况,教务处对初一(1)班学生一周复习的时间进行了调查,复习时间四舍五入后只有4种:1小时,2小时,3小时,4小时,一周复习2小时的女生人数占全班人数的16%,一周复习4小时的男女生人数相等.根据调查结果,制作了两幅不完整的统计图(表):

分组(四舍五入后) | 频数(学生人数) |
1小时 | 2 |
2小时 | a |
3小时 | 4 |
4小时 | b |
初一(1)班女生的复习时间数据(单位:小时)如下:0.9,1.3,1.7,1.8,1.9,2.2,2.2,2.2,2.3,2.4,3.2,3.2,3.2,3.3,3.8,3.9,3.9,4.1,4.2,4.3.
女生一周复习时间频数分布表
(1)四舍五入前,女生一周复习时间的众数为______小时,中位数为______小时;
(2)统计图表中a=______,c=______,初一(1)班男生人数为______人,根据扇形统计图估算初一(1)班男生一周的平均复习时间为______小时;
(3)为了激励学生养成良好的复习习惯,教务处决定对一周复习时间四舍五入后达到3小时及以上的全年级学生进行表扬,每人奖励1个笔记本,初一年级共有1000名学生,请问教务处应该准备大约多少个笔记本?
查看答案和解析>>
科目: 来源: 题型:
【题目】由菜鸟网络打造的一个仓库有相同数量的工人和机器人,均为x名(其中x>5),平时每天都只工作8小时,每名机器人每小时加工包裹(分、拣、包装一体化)的数量是每名工人每小时加工包裹数量的2倍.随着“春节”临近,人工短缺,寄年货的包裹增多,公司决定再增加2名机器人,且将机器人每天工作时间延长至12小时,并对每名机器人进行升级改造,让现在每名机器人每小时加工包裹的数量在原有基础上增加x个,结果现在所有机器人每天加工包裹的数量是所有工人平时每天加工包裹数量的6倍,则该仓库平时一天加工______个包裹.
查看答案和解析>>
科目: 来源: 题型:
【题目】A,C,B三地依次在一条笔直的道路上,甲、乙两车同时分别从A,B两地出发,相向而行,甲车从A地行驶到B地就停止,乙车从B地行驶到A地后立即以相同的速度返回B地,在整个行驶的过程中,甲、乙两车均保持匀速行驶,甲、乙两车距C地的距离之和y(km)与甲车出发的时间t(h)之间的函数关系如图所示,则乙车第二次到达C地时,甲车距B地的距离为______km.
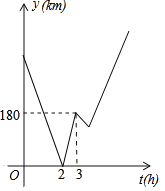
查看答案和解析>>
科目: 来源: 题型:
【题目】为了方便学生在上下学期间安全过马路,南岸区政府决定在南开(融侨)中学校门口修建人行天桥(如图1),其平面图如图2所示,初三(8)班的学生小刘想利用所学知识测量天桥顶棚距地面的高度.天桥入口A点有一台阶AB=2m,其坡角为30°,在AB上方有两段平层BC=DE=1.5m,且BC,DE与地面平行,BC,DE上方又紧接台阶CD,EF,其长度相等且坡度均为i=4:3,顶棚距天桥距离FG=2m,且小刘从入口A点测得顶棚顶端G的仰角为37°,请根据以上数据,帮小刘计算出顶端G点距地面高度为( )m.(结果保留一位小数,参考数据:![]() ≈1.73,sin37°≈
≈1.73,sin37°≈![]() ,cos37°≈
,cos37°≈![]() ,tan37°≈
,tan37°≈![]() )
)
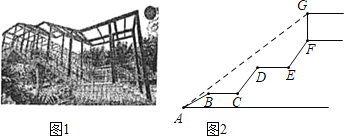
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在边长为2的正方形ABCD中,以B为圆心,AB为半径作扇形ABC,交对角线BD于点E,过点E作⊙B的切线分别交AD,CD于G,F两点,则图中阴影部分的面积为( )
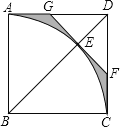
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com