
科目: 来源: 题型:
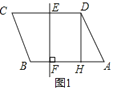
【题目】如图1,在ABCD中,DH⊥AB于点H,CD的垂直平分线交CD于点E,交AB于点F,AB=6,DH=4,BF:FA=1:5.
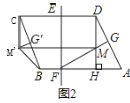
(1)如图2,作FG⊥AD于点G,交DH于点M,将△DGM沿DC方向平移,得到△CG′M′,连接M′B.
①求四边形BHMM′的面积;
②直线EF上有一动点N,求△DNM周长的最小值.
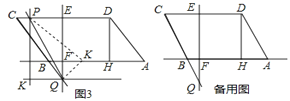
(2)如图3,延长CB交EF于点Q,过点Q作QK∥AB,过CD边上的动点P作PK∥EF,并与QK交于点K,将△PKQ沿直线PQ翻折,使点K的对应点K′恰好落在直线AB上,求线段CP的长.
查看答案和解析>>
科目: 来源: 题型:
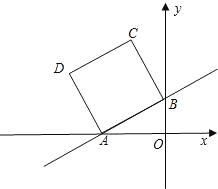
【题目】如图,在平面直角坐标系中,直线y=![]() x+2与x轴、y轴分别交于A、B两点,以AB为边在第二象限内作正方形ABCD.
x+2与x轴、y轴分别交于A、B两点,以AB为边在第二象限内作正方形ABCD.
(1)求点A、B的坐标,并求边AB的长;
(2)求点C和点D的坐标;
(3)在x轴上找一点M,使△MDB的周长最小,请求出M点的坐标,并直接写出△MDB的周长最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】济南某中学在参加“创文明城,点赞泉城”书画比赛中,杨老师从全校30个班中随机抽取了4个班(用A,B,C,D表示),对征集到的作鼎的数量进行了分析统计,制作了两幅不完整的统计图.
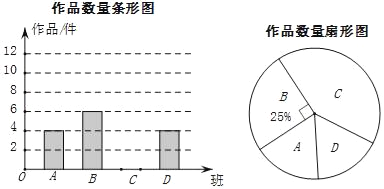
请根据以上信息,回答下列问题:
(l)杨老师采用的调查方式是 (填“普查”或“抽样调查”);
(2)请补充完整条形统计图,并计算扇形统计图中C班作品数量所对应的圆心角度数 .
(3)请估计全校共征集作品的什数.
(4)如果全枝征集的作品中有5件获得一等奖,其中有3名作者是男生,2名作者是女生,现要在获得一样等奖的作者中选取两人参加表彰座谈会,请你用列表或树状图的方法,求恰好选取的两名学生性别相同的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,正方形AOBO2的顶点A的坐标为A(0,2),O1为正方形AOBO2的中心;以正方形AOBO2的对角线AB为边,在AB的右侧作正方形ABO3A1,O2为正方形ABO3A1的中心;再以正方形ABO3A1的对角线A1B为边,在A1B的右侧作正方形A1BB1O4,O3为正方形A1BB1O4的中心;再以正方形A1BB1O4的对角线A1B1为边在A1B1的右侧作正方形A1B1O5A2,O4为正方形A1B1O5A2的中心:…;按照此规律继续下去,则点O2018的坐标为_____.
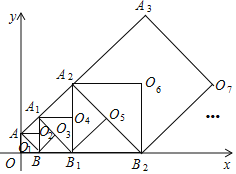
查看答案和解析>>
科目: 来源: 题型:
【题目】已知一次函数y=ax+b过一,二,四象限,且过(6,0),则关于二次函数y=ax2+bx+1的以下说法:①图象与x轴有两个交点;②a<0,b>0;③当x=3时函数有最小值;④若存在一个实数m,当x≤m时,y随x的增大而增大,则m≤3.其中正确的是( )
A. ①②B. ①②③C. ①②④D. ②③④
查看答案和解析>>
科目: 来源: 题型:
【题目】魏晋时期的数学家刘徽首创割圆术.为计算圆周率建立了严密的理论和完善的算法.作圆内接正多边形,当正多边形的边数不断增加时,其周长就无限接近圆的周长,进而可用![]() 来求得较为精确的圆周率.祖冲之在刘徽的基础上继续努力,当正多边形的边数增加24576时,得到了精确到小数点后七位的圆周率,这一成就在当时是领先其他国家一千多年,如图,依据“割圆术”,由圆内接正六边形算得的圆周率的近似值是( )
来求得较为精确的圆周率.祖冲之在刘徽的基础上继续努力,当正多边形的边数增加24576时,得到了精确到小数点后七位的圆周率,这一成就在当时是领先其他国家一千多年,如图,依据“割圆术”,由圆内接正六边形算得的圆周率的近似值是( )
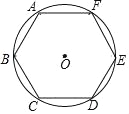
A. 0.5B. 1C. 3D. π
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,O是坐标原点,过点A(﹣1,0)的抛物线y=x2﹣bx﹣3与x轴的另一个交点为B,与y轴交于点C,其顶点为D点.
(1)求b的值以及点D的坐标;
(2)求△BCD的面积;
(3)连接BC、BD、CD,在x轴上是否存在点P,使得以A、C、P为顶点的三角形与△BCD相似?若存在,求出点P的坐标;若不存在,说明理由.
(4)在抛物线上是否存在点Q,使得以A、C、Q为顶点且以AC为直角边的三角形为直角三角形?若存在,求出点Q的坐标;若不存在,说明理由.
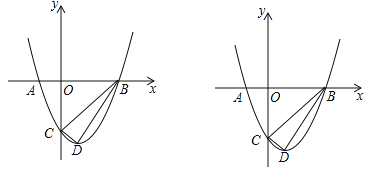
查看答案和解析>>
科目: 来源: 题型:
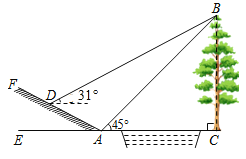
【题目】如图,小明为了测量小河对岸大树BC的高度,他在点A测得大树顶端B的仰角是45°,沿斜坡走![]() 米到达斜坡上点D,在此处测得树顶端点B的仰角为31°,且斜坡AF的坡比为1:2(参考数据:sin31°≈0.52,cos31°≈0.86,tan31°≈0.60).
米到达斜坡上点D,在此处测得树顶端点B的仰角为31°,且斜坡AF的坡比为1:2(参考数据:sin31°≈0.52,cos31°≈0.86,tan31°≈0.60).
(1)求小明从点A走到点D的过程中,他上升的高度;
(2)大树BC的高度约为多少米?
查看答案和解析>>
科目: 来源: 题型:
【题目】在创建“全国文明城市”和“省级文明城区”过程中,栾城区污水处理厂决定先购买A、B两型污水处理设备共20台,对城区周边污水进行处理.已知每台A型设备价格为12万元,每台B型设备价格为10万元;1台A型设备和2台B型设备每周可以处理污水640吨,2台A型设备和3台B型设备每周可以处理污水1080吨.
(1)求A、B两型污水处理设备每周分别可以处理污水多少吨?
(2)要想使污水处理厂购买设备的资金不超过230万元,但每周处理污水的量又不低于4500吨,请你列举出所有购买方案,并指出哪种方案所需资金最少?最少是多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在ABCD中,AE⊥BD,CF⊥BD,E,F分别为垂足.
(1)求证:四边形AECF是平行四边形;
(2)如果AE=3,EF=4,求AF、EC所在直线的距离.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com