
科目: 来源: 题型:
【题目】抛物线y=x2+bx+c经过点A、B、C,已知A(﹣1,0),C(0,﹣3).
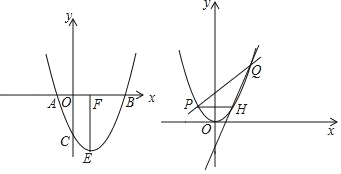
(1)求抛物线的解析式;
(2)如图1,抛物线顶点为E,EF⊥x轴于F点,M(m,0)是x轴上一动点,N是线段EF上一点,若∠MNC=90°,请指出实数m的变化范围,并说明理由.
(3)如图2,将抛物线平移,使其顶点E与原点O重合,直线y=kx+2(k>0)与抛物线相交于点P、Q(点P在左边),过点P作x轴平行线交抛物线于点H,当k发生改变时,请说明直线QH过定点,并求定点坐标.
查看答案和解析>>
科目: 来源: 题型:
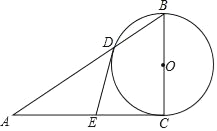
【题目】如图,在Rt△ABC中,∠C=90°,以BC为直径的⊙O交AB于点D,切线DE交AC于点E.
(1)求证:∠A=∠ADE;
(2)若AD=8,DE=5,求BC的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】下表中有两种移动电话计费方式.
月使用费 | 主叫限定时间 | 主叫超时费 | 被叫 | |
方式一 | 49 | 100 |
| 免费 |
方式二 | 69 | 150 |
| 免费 |
设一个月内主叫通话为t分钟![]() 是正整数
是正整数![]() .
.
![]() 当
当![]() 时,按方式一计费为______元;按方式二计费为______元;
时,按方式一计费为______元;按方式二计费为______元;
![]() 当
当![]() 时,是否存在某一时间t,使两种计费方式相等,若存在,请求出对应t的值,若不存在,请说明理由;
时,是否存在某一时间t,使两种计费方式相等,若存在,请求出对应t的值,若不存在,请说明理由;
![]() 当
当![]() 时,请直接写出省钱的计费方式?
时,请直接写出省钱的计费方式?
查看答案和解析>>
科目: 来源: 题型:
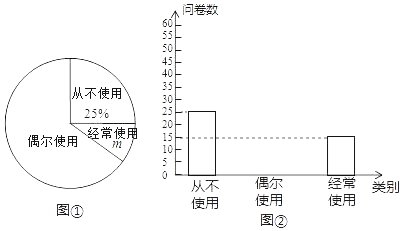
【题目】“低碳生活,绿色出行”是我们倡导的一种生活方式,某校为了解学生对共享单车的使用情况,随机抽取部分学生进行问卷调查,并将这次调查的结果绘制了以下两幅不完整的统计图.
根据所给信息,解答下列问题:
(1)m= ;
(2)补全条形统计图;
(3)这次调查结果的众数是 ;
(4)已知全校共3000名学生,请估计“经常使用”共享单车的学生大约有多少名?
查看答案和解析>>
科目: 来源: 题型:
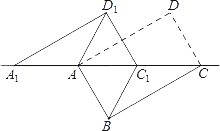
【题目】如图,将矩形ABCD沿对角线AC剪开,再把△ACD沿CA方向平移得到△A1C1D1,连结AD1,BC1.若∠ACB=30°,AB=1,CC1=x,△ACD与△A1C1D1重叠部分的面积为s,则下列结论:①△A1AD1≌△CC1B②当x=1时,四边形ABC1D1是菱形 ③当x=2时,△BDD1为等边三角形 ④s=![]() (x﹣2)2(0<x<2),其中正确的有( )
(x﹣2)2(0<x<2),其中正确的有( )
A. 1 个B. 2 个C. 3 个D. 4 个
查看答案和解析>>
科目: 来源: 题型:
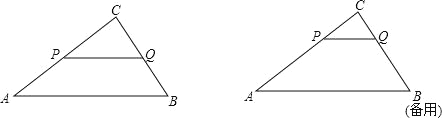
【题目】如图:已知△ABC中,AB=5,BC=3,AC=4,PQ∥AB,P点在AC上(与A、C不重合),Q在BC上.
(1)当△PQC的面积与四边形PABQ的面积相等时,求CP的长;
(2)当△PQC的周长与四边形PABQ的周长相等时,求CP的长;
(3)试问:在AB上是否存在一点M,使得△PQM为等腰直角三角形?若不存在,请简要说明理由;若存在,请求出PQ的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】恩阳区市民广场有一棵高大的老黄角树树.小明为测量该树的高度AD,在大树前的平地上点C处测得大树顶端A的仰角∠C=31°,然后向前直走22米到达B处,又测得大树顶端A的仰角∠ABD=45°,已知C、B、D在同一直线上(如图所示),求老树的高度AD.(参考数据:tan31°≈![]() ,sin31°≈
,sin31°≈![]() )
)


查看答案和解析>>
科目: 来源: 题型:
【题目】阅读材料: 小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如:![]() ,善于思考的小明进行了以下探索:
,善于思考的小明进行了以下探索:
设![]() (其中
(其中![]() 均为整数),则有
均为整数),则有![]() .
.
∴![]() .这样小明就找到了一种把部分
.这样小明就找到了一种把部分![]() 的式子化为平方式的方法.
的式子化为平方式的方法.
请你仿照小明的方法探索并解决下列问题:
当![]() 均为正整数时,若
均为正整数时,若![]() ,用含m、n的式子分别表示
,用含m、n的式子分别表示![]() ,得
,得![]() = ,
= ,![]() = ;
= ;
(2)利用所探索的结论,找一组正整数![]() ,填空: + =( +
,填空: + =( + ![]() )2;
)2;
(3)若![]() ,且
,且![]() 均为正整数,求
均为正整数,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com