
科目: 来源: 题型:
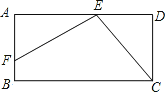
【题目】如图,已知矩形ABCD中,E是AD上一点,F是AB上的一点,EF⊥EC,且EF=EC.
(1)求证:△AEF≌△DCE.
(2)若DE=4cm,矩形ABCD的周长为32cm,求AE的长.
查看答案和解析>>
科目: 来源: 题型:
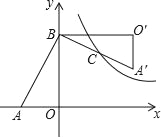
【题目】如图,在Rt△AOB中,直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,将△AOB绕点B逆时针旋转90°后,得到△A′O′B,且反比例函数y=![]() 的图象恰好经过斜边A′B的中点C,若SABO=4,tan∠BAO=2,则k=_____.
的图象恰好经过斜边A′B的中点C,若SABO=4,tan∠BAO=2,则k=_____.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,一个梯子AB长2.5米,顶端A靠在墙AC上,这时梯子下端B与墙角C距离为1.5米,梯子滑动后停在DE的位置上,测得BD长为0.5米,则梯子顶端A下落了( )米.

A. 0.5 B. 1 C. 1.5 D. 2
查看答案和解析>>
科目: 来源: 题型:
【题目】已知正方形ABCD的对角线AC,BD相交于点O.
(1)如图1,E,G分别是OB,OC上的点,CE与DG的延长线相交于点F.若DF⊥CE,求证:OE=OG;
(2)如图2,H是BC上的点,过点H作EH⊥BC,交线段OB于点E,连结DH交CE于点F,交OC于点G.若OE=OG,
①求证:∠ODG=∠OCE;
②当AB=1时,求HC的长.

查看答案和解析>>
科目: 来源: 题型:
【题目】为满足市场需求,某超市在五月初五“端午节”来临前夕,购进一种品牌粽子,每盒进价是40元.超市规定每盒售价不得少于45元.根据以往销售经验发现;当售价定为每盒45元时,每天可以卖出700盒,每盒售价每提高1元,每天要少卖出20盒.
(1)试求出每天的销售量y(盒)与每盒售价x(元)之间的函数关系式;
(2)当每盒售价定为多少元时,每天销售的利润P(元)最大?最大利润是多少?
(3)为稳定物价,有关管理部门限定:这种粽子的每盒售价不得高于58元.如果超市想要每天获得不低于6000元的利润,那么超市每天至少销售粽子多少盒?
查看答案和解析>>
科目: 来源: 题型:
【题目】清明节假期,小红和小阳随爸妈去旅游,他们在景点看到一棵古松树,小红惊讶的说:“呀!这棵树真高!有60多米.”小阳却不以为然:“60多米?我看没有.”两个人争论不休,爸爸笑着说:“别争了,正好我带了一副三角板,用你们学过的知识量一量、算一算,看谁说的对吧!”
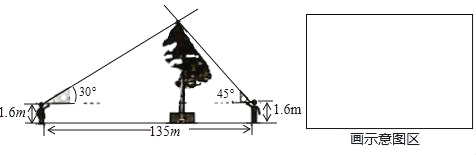
小红和小阳进行了以下测量:如图所示,小红和小阳分别在树的东西两侧同一地平线上,他们用手平托三角板,保持三角板的一条直角边与地平面平行,然后前后移动各自位置,使目光沿着三角板的斜边正好经过树的最高点,这时,测得小红和小阳之间的距离为135米,他们的眼睛到地面的距离都是1.6米.
(1)请在指定区域内画出小红和小阳测量古松树高的示意图;
(2)通过计算说明小红和小阳谁的说法正确(计算结果精确到0.1)(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73,
≈1.73,![]() ≈2.24)
≈2.24)
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读材料:求31+32+33+34+35+36的值
解:设S=31+32+33+34+35+36①
则3S=32+33+34+35+36+37②
用②﹣①得,3S﹣S=(32+33+34+35+36+37)﹣(31+32+33+34+35+36)=37﹣3
∴2S=37﹣3,即S=![]() ,∴31+32+33+34+35+36=
,∴31+32+33+34+35+36=![]()
以上方法我们成为“错位相减法”,请利用上述材料,解决下列问题:
(一)棋盘摆米
这是一个很著名的故事:阿基米德与国王下棋,国王输了,国王问阿基米德要什么奖赏?阿基米德对国王说:“我只要在棋盘上第一格放一粒米,第二格放二粒,第三格放四粒,第四格放八粒…按这个方法放满整个棋盘就行”国王以为要不了多少粮食,就随口答应了,结果国王输了
(1)国际象棋共有64个格子,则在第64格中应放 粒米(用幂表示)
(2)设国王输给阿基米德的米粒数为S,求S
(二)拓广应用:
1.计算:![]() (仿照材料写出求解过程)
(仿照材料写出求解过程)
2.计算:![]() = (直接写出结果)
= (直接写出结果)
查看答案和解析>>
科目: 来源: 题型:
【题目】某学校举行一场知识竞赛活动,竞赛共有4小题,每小题5分,答对给5分,答错或不答给0分,在该学校随机抽取若干同学参加比赛,成绩被制成不完整的统计表如下.
成绩 | 人数(频数) | 百分比(频率) |
0 | ||
5 | 0.2 | |
10 | 5 | |
15 | 0.4 | |
20 | 5 | 0.1 |
根据表中已有的信息,下列结论正确的是( )
A. 共有40名同学参加知识竞赛
B. 抽到的同学参加知识竞赛的平均成绩为10分
C. 已知该校共有800名学生,若都参加竞赛,得0分的估计有100人
D. 抽到同学参加知识竞赛成绩的中位数为15分
查看答案和解析>>
科目: 来源: 题型:
【题目】问题:如图(1),点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,试判断BE、EF、FD之间的数量关系.
【发现证明】小聪把△ABE绕点A逆时针旋转90°至△ADG,从而发现EF=BE+FD,请你利用图(1)证明上述结论.
【类比引申】如图(2),四边形ABCD中,∠BAD≠90°,AB=AD,∠B+∠D=180°,点E、F分别在边BC、CD上,则当∠EAF与∠BAD满足 关系时,仍有EF=BE+FD;请证明你的结论.

【探究应用】如图(3),在某公园的同一水平面上,四条通道围成四边形ABCD.已知AB=AD=80米,∠B=60°,∠ADC=120°,∠BAD=150°,道路BC、CD上分别有景点E、F,且AE⊥AD,DF=40(![]() ﹣1)米,现要在E、F之间修一条笔直道路,求这条道路EF的长.(结果取整数,参考数据:
﹣1)米,现要在E、F之间修一条笔直道路,求这条道路EF的长.(结果取整数,参考数据: ![]() =1.41,
=1.41, ![]() =1.73)
=1.73)
查看答案和解析>>
科目: 来源: 题型:
【题目】小明大学毕业回家乡创业,第一期培植盆景与花卉各50盆售后统计,盆景的平均每盆利润是160元,花卉的平均每盆利润是19元,调研发现:
①盆景每增加1盆,盆景的平均每盆利润减少2元;每减少1盆,盆景的平均每盆利润增加2元;②花卉的平均每盆利润始终不变.
小明计划第二期培植盆景与花卉共100盆,设培植的盆景比第一期增加x盆,第二期盆景与花卉售完后的利润分别为W1,W2(单位:元)
(1)用含x的代数式分别表示W1,W2;
(2)当x取何值时,第二期培植的盆景与花卉售完后获得的总利润W最大,最大总利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com