
科目: 来源: 题型:
【题目】2020年东京奥运会的比赛门票开始接受公众预订.下表为奥运会官方票务网站公布的几种球类比赛的门票的人民币价格,球迷小李用12000元做为预订下表中比赛项目门票的资金.
比赛项目 | 票价(元/场) |
男篮 | 1000 |
足球 | 800 |
乒乓球 | 500 |
(1)若全部资金用来预订男篮门票和乒乓球门票共15张,问男篮门票和乒乓球门票各订多少张?
(2)若在准备资金允许的范围内和总票数不变的前提下,这个球迷想预定上表中三种球类门票,其中足球门票与乒乓球门票数相同,且足球门票的费用不超过男篮门票的费用,问可以预订这三种球类门票各多少张?
查看答案和解析>>
科目: 来源: 题型:
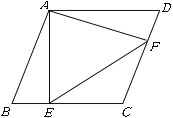
【题目】如图,在菱形ABCD中,∠B=60°,点E、F分别从点B、D出发以同样的速度沿边BC、DC向点![]() 运动.给出以下四个结论:①AE=AF②∠CEF=∠CFE③当点E、F分别为边BC、DC的中点时,△AEF是等边三角形④当点E、F分别为边BC、DC的中点时,△AEF的面积最大.上述结论中正确的序号有________.(把你认为正确的序号都填上)
运动.给出以下四个结论:①AE=AF②∠CEF=∠CFE③当点E、F分别为边BC、DC的中点时,△AEF是等边三角形④当点E、F分别为边BC、DC的中点时,△AEF的面积最大.上述结论中正确的序号有________.(把你认为正确的序号都填上)
查看答案和解析>>
科目: 来源: 题型:
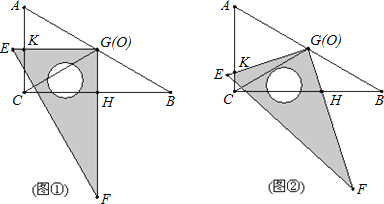
【题目】把两个全等的直角三角板ABC和EFG叠放在一起,使三角板EFG的直角顶点G与三角板ABC的斜边中点O重合,其中∠B=∠F=30°,斜边AB和EF长均为4.
(1)当 EG⊥AC于点K,GF⊥BC于点H时(如图①),求GH:GK的值.
(2) 现将三角板EFG由图①所示的位置绕O点沿逆时针方向旋转,旋转角α满足条件:0°<α<30°(如图②),EG交AC于点K ,GF交BC于点H,GH:GK的值是否改变?证明你发现的结论;
(3)三角板EFG由图①所示的位置绕O点逆时针旋转一周,是否存在某位置使△BFG是等腰三角形,若存在,请直接写出相应的旋转角α(精确到0.1°);若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
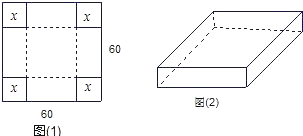
【题目】用一块边长为60㎝的正方形薄钢片制作一个长方体盒子:如果要做成一个没有盖的长方体盒子,可先在薄钢片的四个角上截去四个相同的小正方形,如图(1),然后把四边折合起来,如图(2)
(1)求做成的盒子底面积y(㎝2)与截去小正方形边长x(㎝)之间的函数关系式;
(2)当做成的盒子的底面积为900㎝2时,试求该盒子的容积.
查看答案和解析>>
科目: 来源: 题型:
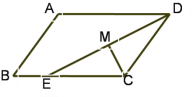
【题目】在平行四边形ABCD中,∠C和∠D的平分线交于M,DM的延长线交AD于E,试猜想:
(1)CM与DE的位置关系?
(2)M在DE的什么位置上?并证明你的猜想.
查看答案和解析>>
科目: 来源: 题型:
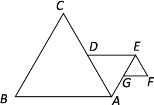
【题目】如图,作等边△ABC,取AC的中点D,以AD为边向△ABC形外作等边△ADE,取AE的中点G,再以EG为边作等边△EFG,如此反复,当作出第6个三角形时,若AB=4,整个图形的外围周长是______.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知抛物线y=﹣x2+bx+c与一直线相交于A(1,0)、C(﹣2,3)两点,与y轴交于点N,其顶点为D.
(1)求抛物线及直线AC的函数关系式;
(2)若P是抛物线上位于直线AC上方的一个动点,求△APC的面积的最大值及此时点P的坐标;
(3)在对称轴上是否存在一点M,使△ANM的周长最小.若存在,请求出M点的坐标和△ANM周长的最小值;若不存在,请说明理由.

查看答案和解析>>
科目: 来源: 题型:
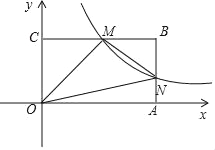
【题目】如图,在平面直角坐标系中,矩形OABC的顶点A、C分别在x、y轴的正半轴上,顶点B的坐标为(4,2).点M是边BC上的一个动点(不与B、C重合),反比例函数y=![]() (k>0,x>0)的图象经过点M且与边AB交于点N,连接MN.
(k>0,x>0)的图象经过点M且与边AB交于点N,连接MN.
(1)当点M是边BC的中点时.
①求反比例函数的表达式;
②求△OMN的面积;
(2)在点M的运动过程中,试证明:![]() 是一个定值.
是一个定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com