
科目: 来源: 题型:
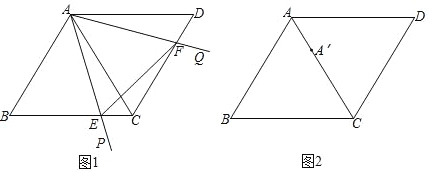
【题目】如图1,AC是边长为6的菱形ABCD的对角线,∠ABC=∠PAQ=60°,∠PAQ绕点A旋转,射线AP、AQ分别交边BC、CD于点E、F,连接EF.请探究:
(1)在旋转过程中,线段AE、AF有怎样的数量关系?并说明理由;
(2)在旋转过程中,△AEF的面积是否存在最小值?若存在,请求出最小值,若不存在,请说明理由
(3)如图2,将∠PAQ沿着AC向下平移至点A处,使CA′:AA′=2:1,在∠PA′Q绕点A′旋转过程中,始终保持∠ABC=∠PA′Q,射线A′P、A′Q分别交直线BC、CD于点E、F,连接EF.当S△A′EF:S菱形ABCD=19:18时,直接写出线段CE的长.
查看答案和解析>>
科目: 来源: 题型:
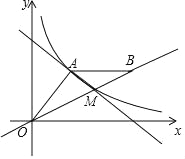
【题目】如图,A(8,6)是反比例函数y=![]() (x>0)在第一象限图象上一点,连接OA,过A作AB∥x轴,且AB=OA(B在A右侧),直线OB交反比例函数y=
(x>0)在第一象限图象上一点,连接OA,过A作AB∥x轴,且AB=OA(B在A右侧),直线OB交反比例函数y=![]() 的图象于点M
的图象于点M
(1)求反比例函数y=![]() 的表达式;
的表达式;
(2)求点M的坐标;
(3)设直线AM关系式为y=nx+b,观察图象,请直接写出不等式nx+b﹣![]() ≤0的解集.
≤0的解集.
查看答案和解析>>
科目: 来源: 题型:
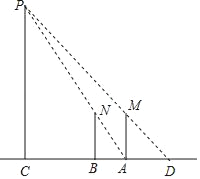
【题目】甲和乙两位同学想测量一下广场中央的照明灯P的高度,如图,当甲站在A处时,乙测得甲的影子长AD正好与他的身高AM相等,接着甲沿AC方向继续向前走,走到点B处时,甲的影子刚好是线段AB,此时测得AB的长为1.2m.已知甲直立时的身高为1.8m,求照明灯的高CP的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】随着信息技术的迅猛发展,人们去商场购物的支付方式更加多样、便捷,在一次购物中,张华和李红都想从“微信”、“支付宝”、“银行卡”、“现金”四种支付方式中选一种方式进行支付.
(1)张华用“微信”支付的概率是______.
(2)请用画树状图或列表法求出两人恰好选择同一种支付方式的概率.(其中“微信”、“支付宝”、“银行卡”、“现金”分别用字母“A”“B”“C”“D”代替)
查看答案和解析>>
科目: 来源: 题型:
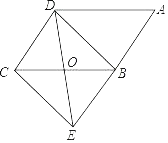
【题目】如图,在ABCD,点O是边BC的中点,连接DO并延长,交AB的延长线于点E,连接BD、EC.
(1)求证:四边形BECD是平行四边形;
(2)若∠BOD=100°,则当∠A= 时,四边形BECD是矩形.
查看答案和解析>>
科目: 来源: 题型:
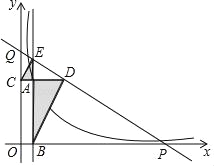
【题目】如图,已知动点A在反比例函数y=![]() (x>0)的图象上,直线PQ与x轴,y轴交于P、Q两点,过点A作CD∥x轴,交y轴于点C,交直线PQ于点D,过点A作EB∥y轴交x轴于点B,交直线PQ于点E,若CE∥BD且CA:AE=1:2,QE:DP=1:9,则阴影部分的面积为______.
(x>0)的图象上,直线PQ与x轴,y轴交于P、Q两点,过点A作CD∥x轴,交y轴于点C,交直线PQ于点D,过点A作EB∥y轴交x轴于点B,交直线PQ于点E,若CE∥BD且CA:AE=1:2,QE:DP=1:9,则阴影部分的面积为______.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,平行四边形ABCD中,对角线AC、BD相交于点O,BD=2AD,E、F、G分别是OC、OD、AB的中点,下列结论:①BE⊥AC;②EG=EF;③△EFG≌△GBE;④EA平分∠GEF;⑤四边形BEFG是菱形.其中正确的个数是( )
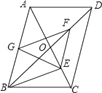
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,正方形ABCD中,E为AB中点,BC=4BF,那么图中与△ADE相似的三角形有( )
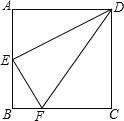
A. △CDFB. △BEFC. △BEF、△DCFD. △BEF,△EDF
查看答案和解析>>
科目: 来源: 题型:
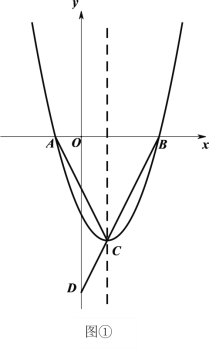
【题目】如图①,二次函数![]() 的图像与
的图像与![]() 轴交于
轴交于![]() 、
、![]() 两点(点
两点(点![]() 在
在![]() 的左侧),顶点为
的左侧),顶点为![]() ,连接
,连接![]() 并延长交
并延长交![]() 轴于点
轴于点![]() ,若
,若![]() .
.
(1)求二次函数的表达式;
(2)在![]() 轴上方有一点
轴上方有一点![]() ,
,![]() ,且
,且![]() ,连接
,连接![]() 并延长交抛物线于点
并延长交抛物线于点![]() ,求点
,求点![]() 的坐标;
的坐标;
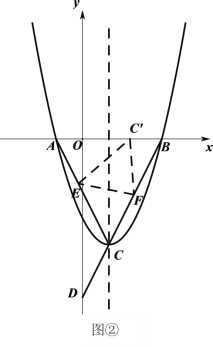
(3)如图②,折叠△![]() ,使点
,使点![]() 落在线段
落在线段![]() 上的点
上的点![]() 处,折痕为
处,折痕为![]() .若△
.若△![]() 有一条边与
有一条边与![]() 轴垂直,直接写出此时点
轴垂直,直接写出此时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目: 来源: 题型:
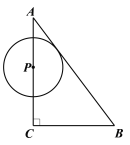
【题目】如图,![]() 中,
中,![]() ,
,![]() ,
,![]() .点
.点![]() 从点
从点![]() 出发,沿着
出发,沿着![]() 运动,速度为
运动,速度为![]() 个单位/
个单位/![]() ,在点
,在点![]() 运动的过程中,以
运动的过程中,以![]() 为圆心的圆始终与斜边
为圆心的圆始终与斜边![]() 相切,设⊙
相切,设⊙![]() 的面积为
的面积为![]() ,点
,点![]() 的运动时间为
的运动时间为![]() (
(![]() )(
)(![]() ).
).
(1)当![]() 时,
时,![]() ;(用含
;(用含![]() 的式子表示)
的式子表示)
(2)求![]() 与
与![]() 的函数表达式;
的函数表达式;
(3)在⊙P运动过程中,当⊙P与三角形ABC的另一边也相切时,直接写出t的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com