
科目: 来源: 题型:
【题目】如图,在正方形纸片![]() 中,对角线
中,对角线![]() 、
、![]() 交于点
交于点![]() ,折叠正方形纸片
,折叠正方形纸片![]() ,使
,使![]() 落在
落在![]() 上,点
上,点![]() 恰好与
恰好与![]() 上的点
上的点![]() 重合.展开后,折痕
重合.展开后,折痕![]() 分别交
分别交![]() 、
、![]() 于点
于点![]() 、
、![]() .连接
.连接![]() .下列结论:①
.下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④四边形
;④四边形![]() 是菱形;⑤
是菱形;⑤![]() .
.
其中正确结论的序号是( )
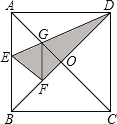
A. ①②③④⑤B. ①②③④C. ①③④⑤D. ①④⑤
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在一张矩形纸片![]() 中,
中,![]() ,
,![]() ,点
,点![]() ,
,![]() 分别在
分别在![]() ,
, ![]() 上,将纸片
上,将纸片![]() 沿直线
沿直线![]() 折叠,点
折叠,点![]() 落在
落在![]() 上的一点
上的一点![]() 处,点
处,点![]() 落在点
落在点![]() 处,有以下四个结论:
处,有以下四个结论:
①四边形![]() 是菱形;②
是菱形;②![]() 平分
平分![]() ;③线段
;③线段![]() 的取值范围为
的取值范围为![]() ;④当点
;④当点![]() 与点
与点![]() 重合时,
重合时,![]() .
.
以上结论中,你认为正确的有( )个.
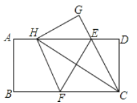
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目: 来源: 题型:
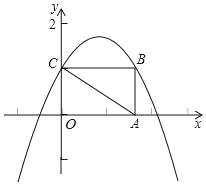
【题目】如图,平面直角坐标系xOy中,矩形OABC的顶点A,C分别在x轴,y轴的正半轴上,且点C的坐标是(0,1),点B的坐标是(![]() ,1),抛物线y=﹣x2+bx+c经过点B和点C.
,1),抛物线y=﹣x2+bx+c经过点B和点C.
(1)求抛物线y=﹣x2+bx+c的表达式:
(2)将△OAC沿直线AC折叠,点O的对称点记为点D,请判断:点D是否在抛物线上?并说明理由;
(3)点E为线段AC上的一个动点.
①若点P在抛物线上,其横坐标为m,当PE⊥AC且PE=![]() 时.请直接写出m的值;
时.请直接写出m的值;
②若点F为线段AB上一个动点,且CE=AF,当OE+OF的值最小时,请直接写出点F的坐标.
查看答案和解析>>
科目: 来源: 题型:
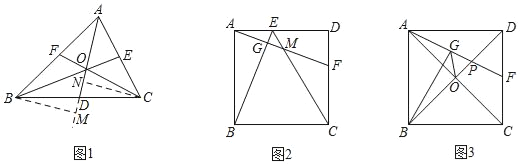
【题目】(探索发现)如图1,△ABC中,点D,E,F分别在边BC,AC,AB上,且AD,BE,CF相交于同一点O.用”S”表示三角形的面积,有S△ABD:S△ACD=BD:CD,这一结论可通过以下推理得到:过点B作BM⊥AD,交AD延长线于点M,过点C作CN⊥AD于点N,可得S△ABD:S△ACD=![]() ,又可证△BDM~△CDN,∴BM:CN=BD:CD,∴S△ABD:S△ACD=BD:CD.由此可得S△BAO:S△BCO= ;S△CAO:S△CBO= ;若D,E,F分别是BC,AC,AB的中点,则S△BFO:S△ABC= .
,又可证△BDM~△CDN,∴BM:CN=BD:CD,∴S△ABD:S△ACD=BD:CD.由此可得S△BAO:S△BCO= ;S△CAO:S△CBO= ;若D,E,F分别是BC,AC,AB的中点,则S△BFO:S△ABC= .
(灵活运用)如图2,正方形ABCD中,点E,F分别在边AD,CD上,连接AF,BE和CE,AF分别交BE,CE于点G,M.
(1)若AE=DF.判断AF与BE的位置关系与数量关系,并说明理由;
(2)若点E,F分别是边AD,CD的中点,且AB=4.则四边形EMFD的面积是 .
(拓展应用)如图3,正方形ABCD中,AB=4,对角线AC,BD相交于点O.点F是边CD的中点.AF与BD相交于点P,BG⊥AF于点G,连接OG,请直接写出S△OGP的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,矩形ABCD的两边AD,AB的长分别为3,8,且B,C在x轴的负半轴上,E是DC的中点,反比例函数y=![]() (x<0)的图象经过点E,与AB交于点F.
(x<0)的图象经过点E,与AB交于点F.
(1)若点B坐标为(﹣6,0),求m的值;
(2)若AF﹣AE=2.且点E的横坐标为a.则点F的横坐标为 (用含a的代数式表示),点F的纵坐标为 ,反比例函数的表达式为 .

查看答案和解析>>
科目: 来源: 题型:
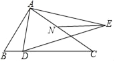
【题目】如图,在Rt△ABC中,∠BAC=90°,BC=5,AB=3,点D是线段BC上一动点,连接AD,以AD为边作△ADE∽△ABC,点N是AC的中点,连接NE,当线段NE最短时,线段CD的长为_____.
查看答案和解析>>
科目: 来源: 题型:
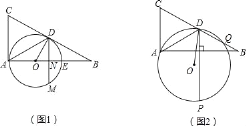
【题目】已知Rt△ABC,∠BAC=90°,点D是BC中点,AD=AC,BC=4![]() ,过A,D两点作⊙O,交AB于点E,
,过A,D两点作⊙O,交AB于点E,
(1)求弦AD的长;
(2)如图1,当圆心O在AB上且点M是⊙O上一动点,连接DM交AB于点N,求当ON等于多少时,三点D、E、M组成的三角形是等腰三角形?
(3)如图2,当圆心O不在AB上且动圆⊙O与DB相交于点Q时,过D作DH⊥AB(垂足为H)并交⊙O于点P,问:当⊙O变动时DP﹣DQ的值变不变?若不变,请求出其值;若变化,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】我们知道不等式的两边加(或减)同一个数(或式子),不等号的方向不变.不等式组是否也具有类似的性质呢?请解答下列问题.
(1)完成下列填空:
已知 | 用“<”或“>”填空 |
| 5+2_____3+1 |
| ﹣3﹣1_____﹣5﹣2 |
| 1﹣2_____4+1 |
(2)一般地,如果![]() 那么a+c_____b+d(用“<”或“>”填空).请你说明上述性质的正确性.
那么a+c_____b+d(用“<”或“>”填空).请你说明上述性质的正确性.
查看答案和解析>>
科目: 来源: 题型:
【题目】某宾馆有若干间住房,住宿记录提供了如下信息:
(1)4月17日全部住满,一天住宿费收入为12000元;
(2)4月18日有20间房空着,一天住宿费收入为9600元;
(3)该宾馆每间房每天收费标准相同.
①一个分式方程,求解该宾馆共有多少间住房,每间住房每天收费多少元?
②通过市场调查发现,每间住房每天的定价每增加10元,就会有5个房间空闲;已知该宾馆空闲房间每天每间支出费用10元,有顾客居住房间每天每间支出费用20元,问房价定为多少元时,该宾馆一天的利润为11000元?(利润=住宿费收入﹣支出费用)
③在(2)的计算基础上,你能发现房价定为多少元时,该宾馆一天的利润最大?请直接写出结论.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知抛物线y=﹣x2+bx+c与一直线相交于A(1,0)、C(﹣2,3)两点,与y轴交于点N,其顶点为D.
(1)求抛物线及直线AC的函数关系式;
(2)若P是抛物线上位于直线AC上方的一个动点,求△APC的面积的最大值及此时点P的坐标;
(3)在对称轴上是否存在一点M,使△ANM的周长最小.若存在,请求出M点的坐标和△ANM周长的最小值;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com