
科目: 来源: 题型:
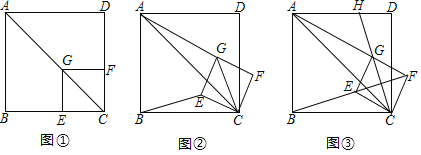
【题目】如图![]() ,已知点G在正方形ABCD的对角线AC上,
,已知点G在正方形ABCD的对角线AC上,![]() ,垂足为点E,
,垂足为点E,![]() ,垂足为点F.
,垂足为点F.
![]() 发现问题:在图
发现问题:在图![]() 中,
中,![]() 的值为______.
的值为______.
![]() 探究问题:将正方形CEGF绕点C顺时针方向旋转
探究问题:将正方形CEGF绕点C顺时针方向旋转![]() 角
角![]() ,如图
,如图![]() 所示,探究线段AG与BE之间的数量关系,并证明你的结论.
所示,探究线段AG与BE之间的数量关系,并证明你的结论.
![]() 解决问题:正方形CEGF在旋转过程中,当B,E,F三点在一条直线上时,如图
解决问题:正方形CEGF在旋转过程中,当B,E,F三点在一条直线上时,如图![]() 所示,延长CG交AD于点H;若
所示,延长CG交AD于点H;若![]() ,
,![]() ,直接写出BC的长度.
,直接写出BC的长度.
查看答案和解析>>
科目: 来源: 题型:
【题目】“食品安全”受到全社会的广泛关注,济南市某中学对部分学生就食品安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两份尚不完整的统计图,请你根据统计图中所提供的信息解答下列问题.
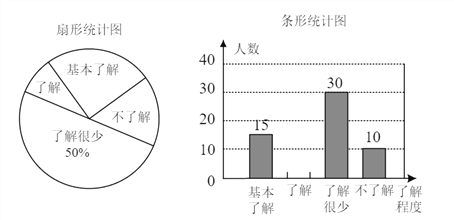
(1)接受问卷调查的学生共有_____人,扇形统计图中“基本了解”部分所对应扇形的圆心角为_____.
(2)请补全条形统计图.
(3)若该中学共有学生900人,请根据上述调查结果,估计该中学学生中对食品安全知识达到“了解”和“基本了解”程度的总人数.
(4)若从对食品安全知识达到“了解”程度的2个女生和2个男生中随机抽取2人参加食品安全知识竞赛,请用树状图或列表法求出恰好抽到1个男生和1个女生的概率.
【答案】(1)60;90°;(2)补图见解析;(3)300;(4)![]()
【解析】分析:(1)根据了解很少的人数除以了解很少的人数所占的百分百求出抽查的总人数,再用“基本了解”所占的百分比乘以360°,即可求出“基本了解”部分所对应扇形的圆心角的度数;(2)用调查的总人数减去“基本了解”“了解很少”和“基本了解”的人数,求出了解的人数,从而补全统计图;(3)用总人数乘以“了解”和“基本了解”程度的人数所占的比例,即可求出达到“了解”和“基本了解”程度的总人数;(4)根据题意列出表格,再根据概率公式即可得出答案.
详解:(1)60;90°.
(2)补全的条形统计图如图所示.
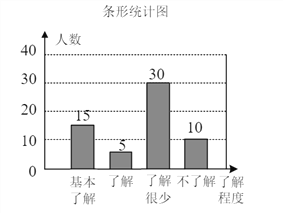
(3)对食品安全知识达到“了解”和“基本了解”的学生所占比例为![]() ,由样本估计总体,该中学学生中对食品安全知识达到“了解”和“基本了解”程度的总人数为
,由样本估计总体,该中学学生中对食品安全知识达到“了解”和“基本了解”程度的总人数为![]() .
.
(4)列表法如表所示,
男生 | 男生 | 女生 | 女生 | |
男生 | 男生男生 | 男生女生 | 男生女生 | |
男生 | 男生男生 | 男生女生 | 男生女生 | |
女生 | 男生女生 | 男生女生 | 女生女生 | |
女生 | 男生女生 | 女生女生 |
所有等可能的情况一共12种,其中选中1个男生和1个女生的情况有8种,所以恰好选中1个男生和1个女生的概率是![]() .
.
点睛:本题考查了条形统计图、扇形统计图以及用列表法或树状图法求概率,根据题意求出总人数是解题的关键;注意运用概率公式:概率=所求情况数与总情况数之比.
【题型】解答题
【结束】
24
【题目】为响应国家全民阅读的号召,某社区鼓励居民到社区阅览室借阅读书,并统计每年的借阅人数和图书借阅总量(单位:本),该阅览室在2015年图书借阅总量是7500本,2017年图书借阅总量是10800本.
(1)求该社区的图书借阅总量从2015年至2017年的年平均增长率.
(2)已知2017年该社区居民借阅图书人数有1350人,预计2018年达到1440人,如果2017年至2018年图书借阅总量的增长率不低于2015年至2017年的年平均增长率,设2018年的人均借阅量比2017年增长a%,求a的值至少是多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】有三张正面分别标有数字![]() ,2,4的不透明卡片,它们除数字外都相同;现将它们背面朝上,洗匀后,从三张卡片中随机地抽出一张,记住数字;
,2,4的不透明卡片,它们除数字外都相同;现将它们背面朝上,洗匀后,从三张卡片中随机地抽出一张,记住数字;
![]() 若把抽出的卡片放回,洗匀后,再从三张卡片中随机抽出一张,记住数字
若把抽出的卡片放回,洗匀后,再从三张卡片中随机抽出一张,记住数字![]() 试用列表或树状图的方法,求两次抽取的卡片上的数字为一正数、一负数的概率.
试用列表或树状图的方法,求两次抽取的卡片上的数字为一正数、一负数的概率.
![]() 若不把抽出的卡片放回,再从剩余两张卡片中随机抽出一张,直接写出两次抽取卡片上的数字为一正数、一负数的概率.
若不把抽出的卡片放回,再从剩余两张卡片中随机抽出一张,直接写出两次抽取卡片上的数字为一正数、一负数的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】.如图 1,B、D 分别是 x 轴和 y 轴的正半轴上的点,AD∥x 轴,AB∥y 轴(AD>AB),点 P 从 C 点出发,以 3cm/s 的速度沿 CDAB 匀速运动,运动到 B 点时终止;点 Q 从 B 点出发,以 2cm/s 的速度,沿 BCD 匀速运动,运动到 D 点时终止.P、Q 两点同时出发, 设运动的时间为 t(s),△PCQ 的面积为 S(cm2),S 与 t 之间的函数关系由图 2 中的曲线段 OE,线段 EF、FG 表示.
(1)求 AD 点的坐标;

(2)求图2中线段FG的函数关系式;
(3)是否存在这样的时间 t,使得△PCQ 为等腰三角形?若存在,直接写出 t 的值;若不存在, 请说明理由.
查看答案和解析>>
科目: 来源: 题型:
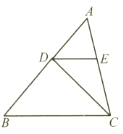
【题目】如图,在△ABC 中,AB=4,D 是 AB 上的一点(不与点 A、B 重合),DE∥BC,交AC 于点 E.设△ABC 的面积为 S,△DEC 的面积为 S'.
(1)当D是AB中点时,求![]() 的值;
的值;
(2)设AD=x,![]() =y,求y与x的函数表达式,并写出自变量x的取值范围;
=y,求y与x的函数表达式,并写出自变量x的取值范围;
(3)根据y的范围,求S-4S′的最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在四边形ABCD中,AB=AD,∠C=90°,以AB为直径的⊙O交AD于点E,CD=ED,连接BD交⊙O于点F.
(1)求证:BC与⊙O相切;
(2)若BD=10,AB=13,求AE的长.

查看答案和解析>>
科目: 来源: 题型:
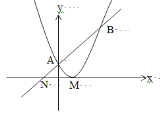
【题目】已知抛物线y=![]() (b<0)的图像的顶点为 M,与 y 轴交于点 A,过点 A的直线 y=x+c 与 x 轴交于点 N,与抛物线另交于点B(6,8).
(b<0)的图像的顶点为 M,与 y 轴交于点 A,过点 A的直线 y=x+c 与 x 轴交于点 N,与抛物线另交于点B(6,8).
(1)求线段 AN 的长;
(3)平移该抛物线得到一条新抛物线.设新抛物线的顶点为 M’.若新抛物线经过点 N,, 且新抛物线的顶点和原抛物线的顶点的连线 MM’平行于直线 AB,求新抛物线对应的函数表达式.
查看答案和解析>>
科目: 来源: 题型:
【题目】郴州市正在创建“全国文明城市”,某校拟举办“创文知识”抢答赛,欲购买A、B两种奖品以鼓励抢答者.如果购买A种20件,B种15件,共需380元;如果购买A种15件,B种10件,共需280元.
(1)A、B两种奖品每件各多少元?
(2)现要购买A、B两种奖品共100件,总费用不超过900元,那么A种奖品最多购买多少件?
查看答案和解析>>
科目: 来源: 题型:
【题目】央视热播节目“朗读者”激发了学生的阅读兴趣.某校为满足学生的阅读需求,欲购进一批学生喜欢的图书,学校组织学生会成员随机抽取部分学生进行问卷调查,被调查学生须从“文史类、社科类、小说类、生活类”中选择自己喜欢的一类,根据调查结果绘制了统计图(未完成),请根据图中信息,解答下列问题:
(1)此次共调查了 名学生;
(2)将条形统计图补充完整;
(3)图2中“小说类”所在扇形的圆心角为 度;
(4)若该校共有学生2500人,估计该校喜欢“社科类”书籍的学生人数.

查看答案和解析>>
科目: 来源: 题型:
【题目】甲、乙两名同学参加1 000米比赛,由于参赛选手较多,将选手随机分A、B、C三组进行比赛.
(1)甲同学恰好在A组的概率是________;
(2)求甲、乙两人至少有一人在B组的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com