
科目: 来源: 题型:
【题目】某饭店推出一种早点套餐,试销一段时间后发现,每份套餐的成本为5元,若每份售价不超过10元,每天可销售400份;若每份售价超过10元,每提高1元,每天的销售量就减少40份,该店每天固定支出费用为600元![]() 不含套餐成本
不含套餐成本![]() 为了便于结算,每份套餐的售价取整数,设每份套餐的售价为
为了便于结算,每份套餐的售价取整数,设每份套餐的售价为![]() 元,该店日销售利润为y元
元,该店日销售利润为y元![]() 日销售利润
日销售利润![]() 每天的销售额
每天的销售额![]() 套餐成本
套餐成本![]() 每天固定支出
每天固定支出![]()
![]() 求y与x的函数关系式并写出自变量的取值范围.
求y与x的函数关系式并写出自变量的取值范围.
![]() 该店要想获得最大日销售利润,又要吸引顾客,使每天销售量较大,按此要求,每份套餐的售价应定为多少元?此时日销售利润为多少元?
该店要想获得最大日销售利润,又要吸引顾客,使每天销售量较大,按此要求,每份套餐的售价应定为多少元?此时日销售利润为多少元?
查看答案和解析>>
科目: 来源: 题型:
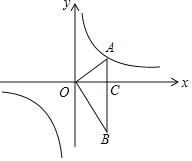
【题目】如图,在平面直角坐标系中,点![]() 在反比例函数
在反比例函数![]() 的图象上,
的图象上,![]() ,
,![]() 轴于点C.
轴于点C.
![]() 求反比例函数
求反比例函数![]() 的表达式;
的表达式;
![]() 求
求![]() 的面积;
的面积;
![]() 若将
若将![]() 绕点B按逆时针方向旋转
绕点B按逆时针方向旋转![]() 得到
得到![]() 点O、A的对应点分别为
点O、A的对应点分别为![]() 、
、![]() ,点
,点![]() 是否在反比例函数
是否在反比例函数![]() 的图象上?若在请直接写出该点坐标,若不在请说明理由.
的图象上?若在请直接写出该点坐标,若不在请说明理由.
查看答案和解析>>
科目: 来源: 题型:
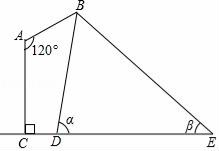
【题目】如图是某路灯在铅垂面内的示意图,灯柱AC的高为11米,灯杆AB与灯柱AC的夹角∠A=120°,路灯采用锥形灯罩,在地面上的照射区域DE长为18米,从D,E两处测得路灯B的仰角分别为α和β,且tanα=6,tanβ=![]() ,求灯杆AB的长度.
,求灯杆AB的长度.
查看答案和解析>>
科目: 来源: 题型:
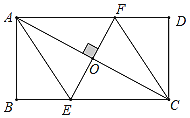
【题目】如图,矩形ABCD的对角线AC的中点为O,过点O作![]() ,交BC边于点E,交AD边于点F,分别连接AE、CF.
,交BC边于点E,交AD边于点F,分别连接AE、CF.
(1)求证:四边形AECF是菱形;
(2)若![]() ,
,![]() ,请直接写出EF的长为__________.
,请直接写出EF的长为__________.
查看答案和解析>>
科目: 来源: 题型:
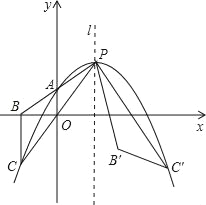
【题目】如图,抛物线y=a(x﹣m﹣1)2+2m(其中m>0)与其对称轴l相交于点P.与y轴相交于点A(0,m)连接并延长PA、PO,与x轴、抛物线分别相交于点B、C,连接BC将△PBC绕点P逆时针旋转,使点C落在抛物线上,设点C、B的对应点分别是点B′和C′.
(1)当m=1时,该抛物线的解析式为: .
(2)求证:∠BCA=∠CAO;
(3)试问:BB′+BC﹣BC′是否存在最小值?若存在,求此时实数m的值,若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
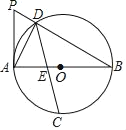
【题目】如图,AB为⊙O的直径,且AB=m(m为常数),点C为![]() 的中点,点D为圆上一动点,过A点作⊙O的切线交BD的延长线于点P,弦CD交AB于点E.
的中点,点D为圆上一动点,过A点作⊙O的切线交BD的延长线于点P,弦CD交AB于点E.
(1)当DC⊥AB时,则![]() = ;
= ;
(2)①当点D在![]() 上移动时,试探究线段DA,DB,DC之间的数量关系;并说明理由;
上移动时,试探究线段DA,DB,DC之间的数量关系;并说明理由;
②设CD长为t,求△ADB的面积S与t的函数关系式;
(3)当![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:如图,BC为⊙O的弦,点A为⊙O上一个动点,△OBC的周长为16.过C作CD∥AB交⊙O于D,BD与AC相交于点P,过点P作PQ∥AB交于Q,设∠A的度数为α.
(1)如图1,求∠COB的度数(用含α的式子表示);
(2)如图2,若∠ABC=90°时,AB=8,求阴影部分面积(用含α的式子表示);
(3)如图1,当PQ=2,求![]() 的值.
的值.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知:AB为⊙O直径,PQ与⊙O交于点C,AD⊥PQ于点D,且AC为∠DAB的平分线,BE⊥PQ于点E.
(1)求证:PQ与⊙O相切;
(2)求证:点C是DE的中点.

查看答案和解析>>
科目: 来源: 题型:
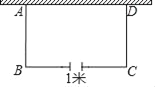
【题目】某农场准备围建一个矩形养鸡场,其中一边靠墙(墙的长度为15米),其余部分用篱笆围成,在墙所对的边留一道1米宽的门,已知篱笆的总长度为23米.
(1)设图中AB(与墙垂直的边)长为x米,则AD的长为 米(请用含x的代数式表示);
(2)若整个鸡场的总面积为y米2,求y的最大值.
查看答案和解析>>
科目: 来源: 题型:
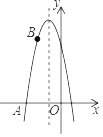
【题目】已知抛物线的对称轴是直线x=﹣1,与x轴一个交点是点A(﹣3,0),且经过点B(﹣2,6)
(1)求该抛物线的解析式;
(2)若点(﹣![]() ,y1)与点(2,y2)都在该抛物线上,直接写出y1与y2的大小关系.
,y1)与点(2,y2)都在该抛物线上,直接写出y1与y2的大小关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com