
科目: 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,以AC为直径作⊙O交AB于点D,E为BC的中点,连接DE并延长交AC的延长线于点F.
(1)求证:DE是⊙O的切线;
(2)若CF=2,DF=4,求⊙O直径的长.

查看答案和解析>>
科目: 来源: 题型:
【题目】传统节日“元宵节”时,小丽的妈妈为小丽盛了一碗汤圆,其中一个汤圆是花生馅,一个汤圆是黑芝麻馅,两个汤圆草莓馅,这4个汤圆除了内部馅料不同外,其他均相同.
(1)若小丽随意吃一个汤圆,刚好吃到黑芝麻馅的概率是多少?
(2)小丽喜欢草莓馅的汤圆,妈妈在盛了4个汤圆后,又为小丽多盛了2个草莓馅的汤圆,若小丽吃2个汤圆,都是草莓馅的概率是多少?
查看答案和解析>>
科目: 来源: 题型:
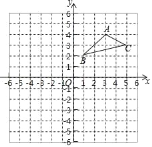
【题目】如图,在平面直角坐标系中,△ABC的三个顶点分别是A(3,4)、B(1,2)、C(5,3)
(1)将△ABC平移,使得点A的对应点A1的坐标为(﹣2,4),在如图的坐标系中画出平移后的△A1B1C1;
(2)将△A1B1C1绕点C1逆时针旋转90°,画出旋转后的△A2B2C1并直接写出A2、B2的坐标;
(3)求△A2B2C1的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c经过点(﹣1,0),对称轴为直线l,则下列结论:①abc>0;②a+b+c>0;③a+c>0;④a+b>0,正确的是( )

A. ①②④B. ②④C. ①③D. ①④
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,△ABC中,∠CAB=70°,在同一平面内,将△ABC绕点A旋转到△AB'C'的位置,使得C′C∥AB,则∠CAB'等于( )
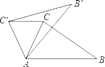
A. 30°B. 25°C. 15°D. 10°
查看答案和解析>>
科目: 来源: 题型:
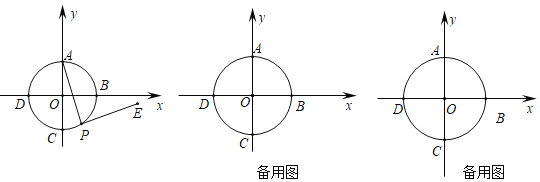
【题目】如图,半径为4且以坐标原点为圆心的圆O交x轴,y轴于点B、D、A、C,过圆上的动点![]() 不与A重合
不与A重合![]() 作
作![]() ,且
,且![]() 在AP右侧
在AP右侧![]() .
.
![]() 当P与C重合时,求出E点坐标;
当P与C重合时,求出E点坐标;
![]() 连接PC,当
连接PC,当![]() 时,求点P的坐标;
时,求点P的坐标;
![]() 连接OE,直接写出线段OE的取值范围.
连接OE,直接写出线段OE的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:如图1,抛物线的顶点为M,平行于x轴的直线与该抛物线交于点A,B(点A在点B左侧),根据对称性△AMB恒为等腰三角形,我们规定:当△AMB为直角三角形时,就称△AMB为该抛物线的“完美三角形”.

(1)①如图2,求出抛物线![]() 的“完美三角形”斜边AB的长;
的“完美三角形”斜边AB的长;
②抛物线![]() 与
与![]() 的“完美三角形”的斜边长的数量关系是 ;
的“完美三角形”的斜边长的数量关系是 ;
(2)若抛物线![]() 的“完美三角形”的斜边长为4,求a的值;
的“完美三角形”的斜边长为4,求a的值;
(3)若抛物线![]() 的“完美三角形”斜边长为n,且
的“完美三角形”斜边长为n,且![]() 的最大值为-1,求m,n的值.
的最大值为-1,求m,n的值.
查看答案和解析>>
科目: 来源: 题型:
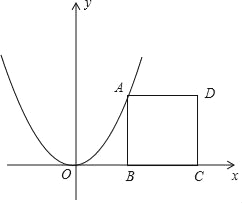
【题目】如图,正方形ABC的顶点A在抛物线y=x2上,顶点B,C在x轴的正半轴上,且点B的坐标为(1,0)
(1)求点D坐标;
(2)将抛物线y=x2适当平移,使得平移后的抛物线同时经过点B与点D,求平移后抛物线解析式,并说明你是如何平移的.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,某消防队在一居民楼前进行演习,消防员利用云梯成功救出点B处的求救者后,又发现点B正上方点C处还有一名求救者.在消防车上点A处测得点B和点C的仰角分别是45°和65°,点A距地面2.5米,点B距地面10.5米.为救出点C处的求救者,云梯需要继续上升的高度BC约为多少米?(结果保留整数.参考数据:tan65°≈2.1,sin65°≈0.9,cos65°≈0.4,![]() ≈1.4)
≈1.4)

查看答案和解析>>
科目: 来源: 题型:
【题目】一只箱子里共有3个球,其中2个白球,1个红球,它们除颜色外均相同。
(1)从箱子中任意摸出一个球是白球的概率是多少?
(2)从箱子中任意摸出一个球,不将它放回箱子,搅匀后再摸出一个球,求两次摸出球的都是白球的概率,并画出树状图。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com