
科目: 来源: 题型:
【题目】在圆O中,弦AB与CD相交于点E,且弧AC与弧BD相等.点D在劣弧AB上,联结CO并延长交线段AB于点F,联结OA、OB.当OA=![]() ,且tan∠OAB=
,且tan∠OAB=![]() .
.
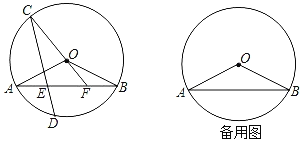
(1)求弦CD的长;
(2)如果△AOF是直角三角形,求线段EF的长;
(3)如果S△CEF=4S△BOF,求线段AF的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知一个抛物线经过A(0,1),B(1,3),C(﹣1,1)三点.
(1)求这个抛物线的表达式及其顶点D的坐标;
(2)联结AB、BC、CA,求tan∠ABC的值;
(3)如果点E在该抛物线的对称轴上,且以点A、B、C、E为顶点的四边形是梯形,直接写出点E的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:如图,△ABC中,∠ACB=90°,D在斜边AB上,DE⊥AC,DF⊥BC,垂足分别为E,F.
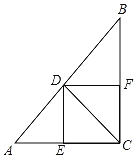
(1)当∠ACD=∠BCD时,求证:四边形DECF是正方形;
(2)当∠BCD=∠A时,求证:![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】如果三角形的两个内角∠α与∠β满足2α+β=90°,那么,我们将这样的三角形称为“准互余三角形”.在△ABC中,已知∠C=90°,BC=3,AC=4(如图所示),点D在AC边上,联结BD.如果△ABD为“准互余三角形”,那么线段AD的长为_____(写出一个答案即可).

查看答案和解析>>
科目: 来源: 题型:
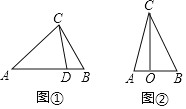
【题目】如图①在![]() 中,若点
中,若点![]() 在边
在边![]() 上,且
上,且![]() 则点
则点![]() 定义为
定义为![]() 的边
的边![]() 上的“金点”.
上的“金点”.
![]() 已知点
已知点![]() 是
是![]() 的边
的边![]() 上的“金点”:
上的“金点”:
①若![]() 则
则![]() 的长为 _;
的长为 _;
②若![]() 则
则![]() 的长为 _;
的长为 _;
![]() 在图①中,若点
在图①中,若点![]() 是
是![]() 的边
的边![]() 的中点,
的中点,![]() 试判断点
试判断点![]() 是不是
是不是![]() 的“金
的“金
点”,并说明理由;
![]() 如图②,已知点
如图②,已知点![]() 为同一直线上三点,且
为同一直线上三点,且![]() 在
在![]() 所在直线上是否存在一点
所在直线上是否存在一点![]() 使点
使点![]() 中的某一点是其余三点围成的三角形的“金点”.若存在,求出线段
中的某一点是其余三点围成的三角形的“金点”.若存在,求出线段![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线![]() :
:![]() 的项点为
的项点为![]() ,交
,交![]() 轴于
轴于![]() 、
、![]() 两点(
两点(![]() 点在
点在![]() 点左侧),且
点左侧),且![]() .
.
(1)求抛物线![]() 的函数解析式;
的函数解析式;
(2)过点![]() 的直线交抛物线于点
的直线交抛物线于点![]() ,交
,交![]() 轴于点
轴于点![]() ,若
,若![]() 的面积被
的面积被![]() 轴分为1: 4两个部分,求直线
轴分为1: 4两个部分,求直线![]() 的解析式;
的解析式;
(3)在(2)的情况下,将抛物线![]() 绕点
绕点![]() 逆时针旋转180°得到抛物线
逆时针旋转180°得到抛物线![]() ,点
,点![]() 为抛物线
为抛物线![]() 上一点,当点
上一点,当点![]() 的横坐标为何值时,
的横坐标为何值时,![]() 为直角三角形?
为直角三角形?
查看答案和解析>>
科目: 来源: 题型:
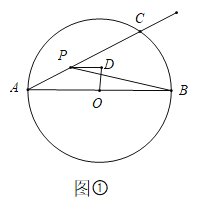
【题目】如图①线段![]() 是
是![]() 的直径,
的直径,![]() 点
点![]() 在
在![]() 上,
上,![]() 点
点![]() 在射线
在射线![]() 上运动(点
上运动(点![]() 不与点
不与点![]() 重合),直径
重合),直径![]() 的垂线
的垂线![]() 与
与![]() 的平行线
的平行线![]() 相交于点
相交于点![]() 连接
连接![]() 设
设![]()
![]() 求
求![]() 的取值范围;
的取值范围;
![]() 如图②点
如图②点![]() 是线段
是线段![]() 与
与![]() 的交点,若
的交点,若![]() 求证:直线
求证:直线![]() 与
与![]() 相切;
相切;

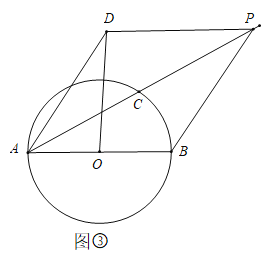
![]() 如图③当
如图③当![]() 时,连接
时,连接![]() 判断四边形
判断四边形![]() 的形状,并说明理由.
的形状,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
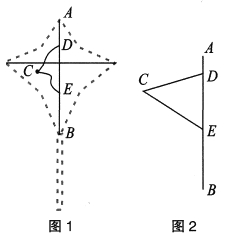
【题目】清代诗人高鼎的诗句“儿童散学归来早,忙趁东风放纸鸢”描绘出一幅充满生机的春天景象.小明制作了一个风筝,如图 1 所示,AB 是风筝的主轴,在主轴 AB上的 D、E 两处分别固定一根系绳,这两根系绳在 C 点处打结并与风筝线连接.如图 2,根据试飞,将系绳拉直后,当∠CDE=75°,∠CED=60°时,放飞效果佳.已知 D、E 两点之间的距离为 20cm,求两根系绳 CD、CE 的长. (结果保留整数,不计打结长度.参考数据:![]() )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】为响应市政府关于“垃圾不落地,市区更美丽”的主题宣传活动,某校随机调查了部分学生对垃圾分类知识的了解情况,对该校部分学生进行了问卷调查,并将调查结果分为![]() 四类(其中
四类(其中![]() 类表示“非常了解”,
类表示“非常了解”,![]() 类表示“比较了解”,
类表示“比较了解”,![]() 类表示“基本了解”,
类表示“基本了解”,![]() 类表示“不太了解”).根据调查结果得到如下不完整的统计表和统计图.请解答下列问题:
类表示“不太了解”).根据调查结果得到如下不完整的统计表和统计图.请解答下列问题:
了解程度 | 人数(人) | 所占百分比 |
|
|
|
|
|
|
|
|
|
|
|
|
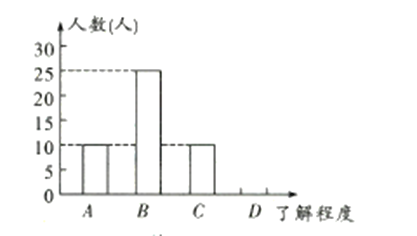
![]() ,
,![]() .
.
![]() 补全条形统计图;
补全条形统计图;
![]() 若该校共有学生
若该校共有学生![]() 人,估计该校对垃圾分类知识“非常了解”的有多少人?
人,估计该校对垃圾分类知识“非常了解”的有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com