
科目: 来源: 题型:
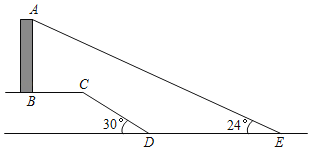
【题目】如图,要测量一垂直于水平面的建筑物AB的高度,小明从建筑物底端B出发,沿水平方向向右走30米到达点C,又经过一段坡角为30°,长为20米的斜坡CD,然后再沿水平方向向右走了50米到达点E(A,B,C,D,E均在同一平面内).在E处测得建筑物顶端A的仰角为24°,求建筑物AB的高度.(结果保留根号,参考数据:sin24°≈![]() ,cos24°≈
,cos24°≈![]() ,tan24°=
,tan24°=![]() )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】一个盒子中装有2个红球,1个白球和1个蓝球,这些球除颜色外都相同,小明和小凡准备用这些球做游戏,游戏规则如下:从盒子中随机摸出一个球,记下颜色后放回,再从中随机摸出一个球,若两次摸到的球的颜色都是红色,小明胜;若两次摸到的球的颜色能配成紫色,则小凡胜,这个游戏对双方公平吗?请说明理由.
查看答案和解析>>
科目: 来源: 题型:
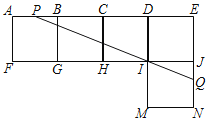
【题目】如图,一“L”型纸片是由5个边长都是10cm的正方形拼接而成,过点I的直线分别与AE,JN交于点P,Q,且“L”型纸片被直线PQ分成面积相等的上下两部分,将该纸片沿BG,CH,DI,IJ折成一个无盖的正方体盒子后,点P,Q之间的距离为_____cm.
查看答案和解析>>
科目: 来源: 题型:
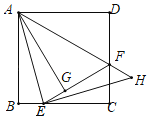
【题目】如图,已知正方形ABCD的边长为3,E是边BC上一点,BE=1,将△ABE,△ADF分别沿折痕AE,AF向内折叠,点B,D在点G处重合,过点E作EH⊥AE,交AF的延长线于H,则线段FH的长为_______.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系中,抛物线![]() 的最高点的纵坐标是2.
的最高点的纵坐标是2.

(1)求抛物线的表达式;
(2)将抛物线在![]() 之间的部分记为图象
之间的部分记为图象![]() ,将图象
,将图象![]() 沿直线x=1翻折,翻折后图象记为
沿直线x=1翻折,翻折后图象记为![]() ,图象
,图象![]() 和
和![]() 组成G,直线
组成G,直线![]() :
:![]()
![]() 和图象G在x轴上方的部分有两个公共点,求k的取值范围;
和图象G在x轴上方的部分有两个公共点,求k的取值范围;
(3)直线![]() :
:![]() 与图象G在x轴上方的部分分别交于A、M、P、Q四点,若AM=2PQ,求
与图象G在x轴上方的部分分别交于A、M、P、Q四点,若AM=2PQ,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】在△ABC中,∠ACB=90°,AC=BC,点P在边AB上,点D、Q分别为边BC上的点,线段AD的延长线与线段PQ的延长线交于点F,连接CP交AF于点E,若∠BPF=∠APC,FD=FQ.
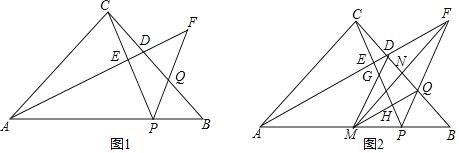
(1)如图1,求证:AF⊥CP;
(2)如图2,作∠AFP的平分线FM交AB于点M,交BC于点N,若FN=MN,求证:![]() ;
;
(3)在(2)的条件下,连接DM、MQ,分别交PC于点G、H,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某市精准扶贫工作已经进入攻坚阶段,贫困的张大爷在某单位的帮扶下,把一片坡地改造后种植了大樱桃.今年正式上市销售,在销售30天中,第一天卖出20千克,为了扩大销量,在一段时间内采取降价措施,每天比前一天多卖出4千克.当售价不变时,销售量也不发生变化.已知种植销售大樱桃的成本为18元/千克,设第![]() 天的销售价
天的销售价![]() 元/千克,
元/千克,![]() 与
与![]() 函数关系如下表:
函数关系如下表:
表一
天数 | 1 | 2 | 3 | …… | …… | 20 |
售价(元/千克) | 37.5 | 37 | 36.5 | …… | …… | 28 |
表二
天数 | 21 | 22 | …… | …… | 30 |
售价(元/千克) | 28 | 28 | …… | …… | 28 |
(1)求![]() 与
与![]() 函数解析式;
函数解析式;
(2)求销售大樱桃第几天时,当天的利润最大?最大利润是多少?
(3)销售大樱桃的30天中,当天利润不低于
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,以AB为直径作圆交AC、BC于点D、E两点,AF切⊙O于点A,点D是AC中点.
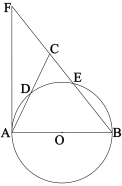
(1)求证:AB=BC;
(2)若![]() ,CF=
,CF=![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,直线![]() 与反比例函数
与反比例函数![]() 的图象交于A(-1,3),B(3,
的图象交于A(-1,3),B(3,![]() )两点,过点A作AC⊥x轴于点C,过点B作BD⊥x轴于点D.
)两点,过点A作AC⊥x轴于点C,过点B作BD⊥x轴于点D.

(1)求一次函数及反比例函数的解析式;
(2)若点P在直线![]() 上,且S△ACP=2S△BDP,求点P的坐标.
上,且S△ACP=2S△BDP,求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com