
科目: 来源: 题型:
【题目】已知二次函数![]() 的图象过点
的图象过点![]() 且与直线
且与直线![]() 相交于
相交于![]() 、
、![]() 两点,点
两点,点![]() 在
在![]() 轴上,点
轴上,点![]() 在
在![]() 轴上.
轴上.
![]() 求二次函数的解析式.
求二次函数的解析式.
![]() 如果
如果![]() 是线段
是线段![]() 上的动点,
上的动点,![]() 为坐标原点,试求
为坐标原点,试求![]() 的面积
的面积![]() 与
与![]() 之间的函数关系式,并求出自变量的取值范围.
之间的函数关系式,并求出自变量的取值范围.
![]() 是否存在这样的点
是否存在这样的点![]() ,使
,使![]() ?若存在,求出点
?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知A0 A1= A1A2= A2A3…,图中的螺旋形由一系列直角三角形组成,则第n个三角形的面积为_________,周长为___________.
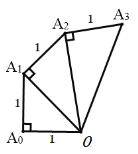
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 与点
与点![]() 关于
关于![]() 轴对称,点
轴对称,点![]() 的坐标为
的坐标为![]() ,过点
,过点![]() 作
作![]() 轴的垂线
轴的垂线![]() 交抛物线于点
交抛物线于点![]() .
.
(1)求点![]() 、点
、点![]() 、点
、点![]() 的坐标;
的坐标;
(2)当点![]() 在线段
在线段![]() 上运动时,直线
上运动时,直线![]() 交
交![]() 于点
于点![]() ,试探究当
,试探究当![]() 为何值时,四边形
为何值时,四边形![]() 是平行四边形;
是平行四边形;
(3)在点![]() 的运动过程中,是否存在点
的运动过程中,是否存在点![]() ,使
,使![]() 是以
是以![]() 为直角边的直角三角形?若存在,求出点
为直角边的直角三角形?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】(1)问题发现
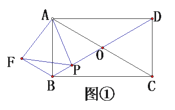
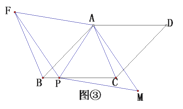
如图①,矩形![]() 的对角线
的对角线![]() 交于点
交于点![]() ,且
,且![]() ,点
,点![]() 为线段
为线段![]() 上任意一点,以
上任意一点,以![]() 为边作等边三角形
为边作等边三角形![]() ,连接
,连接![]() ,则
,则![]() 与
与![]() 之间的数量关系是 ;
之间的数量关系是 ;
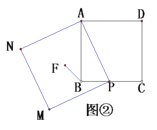
(2)类比延伸
如图②,在正方形![]() 中,点
中,点![]() 为
为![]() 边上任意一点,以
边上任意一点,以![]() 为边作正方形
为边作正方形![]() ,
,![]() 为正方形
为正方形![]() 的中心,连接
的中心,连接![]() ,直接写出
,直接写出![]() 与
与![]() 的数量关系为 ;
的数量关系为 ;
(3)拓展迁移
如图③,在菱形![]() 中,
中,![]() ,点
,点![]() 为
为![]() 边上一点,以
边上一点,以![]() 为对角线作菱形
为对角线作菱形![]() ,满足
,满足![]() ,连接
,连接![]() ,猜想
,猜想![]() 与
与![]() 的数量关系,并证明你的结论.
的数量关系,并证明你的结论.
查看答案和解析>>
科目: 来源: 题型:
【题目】小亮和爸爸登山,两人距地面的高度![]() (米)与小亮登山时间
(米)与小亮登山时间![]() (分)之间的函数图象分别如图中折线
(分)之间的函数图象分别如图中折线![]() 和线段
和线段![]() 所示,根据函数图形进行一下探究:
所示,根据函数图形进行一下探究:

(1)设线段![]() 所表示的函数关系式为
所表示的函数关系式为![]() ,根据图象求
,根据图象求![]() 的值,并写出
的值,并写出![]() 的实际意义;
的实际意义;
(2)若小亮提速后,他登山的速度是爸爸速度的3倍,问:小亮登山多长时间时开始提速?此时小亮距地面的高度是多少米?
查看答案和解析>>
科目: 来源: 题型:
【题目】为了解某校九年级男生的体能状况,体育老师随机抽取部分男生进行引体向上测试,并对成绩进行统计,绘制成图(1)和图(2)两幅尚不完整的统计图.
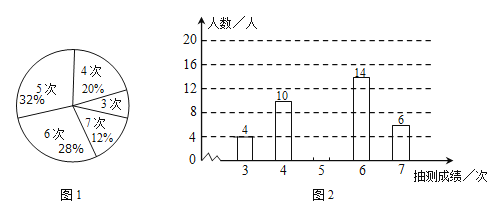
(1)本次抽取的男生有 人,抽取成绩的众数是 ;
(2)请你在图(2)补充完整;
(3)若规定引体向上5次以上(含5次)为体能达标,该校九年级男生共有900人,则估计有多少人体能达标?
查看答案和解析>>
科目: 来源: 题型:
【题目】黄石市在创建国家级文明卫生城市中,绿化档次不断提升.某校计划购进A,B两种树木共100棵进行校园绿化升级,经市场调查:购买A种树木2棵,B种树木5棵,共需600元;购买A种树木3棵,B种树木1棵,共需380元.
(1)求A种,B种树木每棵各多少元?
(2)因布局需要,购买A种树木的数量不少于B种树木数量的3倍.学校与中标公司签订的合同中规定:在市场价格不变的情况下(不考虑其他因素),实际付款总金额按市场价九折优惠,请设计一种购买树木的方案,使实际所花费用最省,并求出最省的费用.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,已知在平面直角坐标系![]() 中,点
中,点![]() 、
、![]() 、
、![]() 分别为坐标轴上的三个点,且
分别为坐标轴上的三个点,且![]() ,
,![]() ,
,![]() .
.
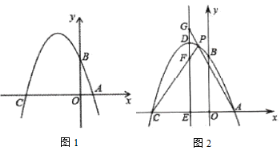
(1)求经过![]() 、
、![]() 、
、![]() 三点的抛物线的解析式;
三点的抛物线的解析式;
(2)点![]() 是抛物线上一个动点,且在直线
是抛物线上一个动点,且在直线![]() 的上方,连接
的上方,连接![]() 、
、![]() ,并把
,并把![]() 沿
沿![]() 翻折,得到四边形
翻折,得到四边形![]() ,那么是否存在点,使四边形
,那么是否存在点,使四边形![]() 为菱形?若存在,请求出此时点
为菱形?若存在,请求出此时点![]() 的坐标;若不存在,请说明理由;
的坐标;若不存在,请说明理由;
(3)如图2,过抛物线顶点![]() 作直线
作直线![]() 轴,交
轴,交![]() 轴于点
轴于点![]() ,点
,点![]() 是抛物线上
是抛物线上![]() 、
、![]() 两点间的一个动点(点
两点间的一个动点(点![]() 不与
不与![]() 、
、![]() 两点重合),直线
两点重合),直线![]() 、
、![]() 与直线
与直线![]() 分别交于点
分别交于点![]() 、
、![]() ,当点
,当点![]() 运动时,
运动时,![]() 是否为定值?若是,试求出该定值;若不是,请说明理由.
是否为定值?若是,试求出该定值;若不是,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】(新洲区月考)如图1,AB为半圆O的直径,C为圆弧上一点,过点C的直线与AB的延长线交于点E,AD⊥CE于点D,AC平分∠DAB.
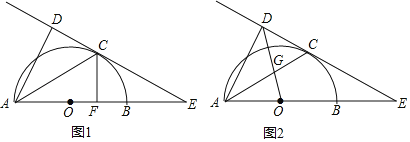
(1)求证:CE是⊙O的切线.
(2)若AB=6,B为OE的中点,CF⊥AB,垂足为点F,求CF的长;
(3)如图2,连接OD交AC于点G,若![]() ,求sinE的值.
,求sinE的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】春天来了,我校计划组织师生共![]() 人坐
人坐![]() 、
、![]() 两种型号的大巴车外出春游,且
两种型号的大巴车外出春游,且![]() 型车每辆租金为
型车每辆租金为![]() 元,
元,![]() 型车每辆租金为
型车每辆租金为![]() 元,为了保证安全,校方要求必须保证人人都有座位.学生南南发现若租
元,为了保证安全,校方要求必须保证人人都有座位.学生南南发现若租![]() 辆
辆![]() 型与
型与![]() 辆
辆![]() 型大巴车恰好能坐下
型大巴车恰好能坐下![]() 人,若租
人,若租![]() 辆
辆![]() 型与
型与![]() 辆
辆![]() 型大巴车恰好能坐下
型大巴车恰好能坐下![]() 人.
人.
(1)请问![]() 辆
辆![]() 型与
型与![]() 辆
辆![]() 型大巴车各有几座?
型大巴车各有几座?
(2)现学校决定租两种型号的大巴车共![]() 辆作为出行交通工具,但政教主任蒋老师发现租车总经费不能超过
辆作为出行交通工具,但政教主任蒋老师发现租车总经费不能超过![]() 元.他想运用函数的知识进行分析,为学校寻找最节省的租车方案.现蒋老师设学校租了
元.他想运用函数的知识进行分析,为学校寻找最节省的租车方案.现蒋老师设学校租了![]() 型大巴车
型大巴车![]() 辆,租车总费用为
辆,租车总费用为![]() 元.请你帮蒋老师完成分析过程,确定共有几种租车方案?哪种租车方案最省钱?并求出最低费用.
元.请你帮蒋老师完成分析过程,确定共有几种租车方案?哪种租车方案最省钱?并求出最低费用.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com