
科目: 来源: 题型:
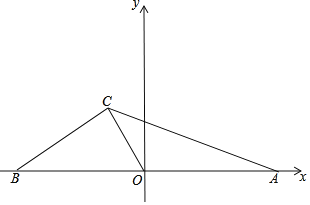
【题目】如图,在平面直角坐标系中,直线BC:y=![]() 交x轴于点B,点A在x轴正半轴上,OC为△ABC的中线,C的坐标为(m,
交x轴于点B,点A在x轴正半轴上,OC为△ABC的中线,C的坐标为(m,![]() )
)
(1)求线段CO的长;
(2)点D在OC的延长线上,连接AD,点E为AD的中点,连接CE,设点D的横坐标为t,△CDE的面积为S,求S与t的函数解析式;
(3)在(2)的条件下,点F为射线BC上一点,连接DB、DF,且∠FDB=∠OBD,CE=![]() ,求此时S值及点F坐标.
,求此时S值及点F坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知△ABC内接于⊙O,AD平分∠BAC交⊙O于点D,交BC于点K,连接DB、DC.
(1)如图1,求证:DB=DC;
(2)如图2,点E、F在⊙O上,连接EF交DB、DC于点G、H,若DG=CH,求证:EG=FH;
(3)如图3,在(2)的条件下,BC经过圆心O,且AD⊥EF,BM平分∠ABC交AD于点M,DK=![]() BM,连接GK、HK、CM,若△BDK与△CKM的面积差为1,求四边形DGKH的面积.
BM,连接GK、HK、CM,若△BDK与△CKM的面积差为1,求四边形DGKH的面积.

查看答案和解析>>
科目: 来源: 题型:
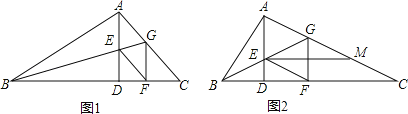
【题目】在△ABC中,∠BAC=90°,AD⊥BC于D,BG平分∠ABC交AD于E,交AC于G,GF⊥BC于F,连接EF.
(1)如图1,求证:四边形AEFG是菱形;
(2)如图2,若E为BG的中点,过点E作EM∥BC交AC于M,在不添加任何辅助线的情况下,请直接写出图2中是CM长![]() 倍的所有线段.
倍的所有线段.
查看答案和解析>>
科目: 来源: 题型:
【题目】时下娱乐综艺节目风靡全国,随机对九年级部分学生进行了一次调查,对最喜欢《我是喜剧王》(记为A)、《王牌对王牌》(记为B)、《奔跑吧,兄弟》(记为C)、《欢乐喜剧人》(记为D)的同学进行了统计(每位同学只选择一个最喜欢的节目),绘制了以下不完整的统计图,请根据图中信息解答问题:
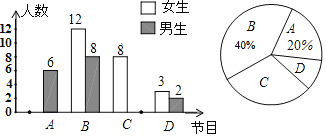
(1)求本次调查一共选取了多少名学生;
(2)将条形统计图补充完整;
(3)若九年级共有1900名学生,估计其中最喜欢《奔跑吧,兄弟》的学生大约是多少名.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,点O为坐标原点,直线y=﹣x+6与x轴交于点A,与y轴交于点B,在x轴上有一点E,在y轴上有一点F,满足OB=3BF=3AE,连接EF,交AB于点M,则M的坐标为_____.
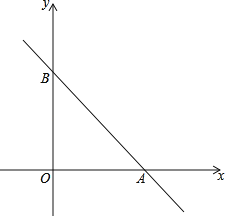
查看答案和解析>>
科目: 来源: 题型:
【题目】甲、乙两个工程队共同承担一项筑路任务,甲队单独施工完成此项任务比乙队单独施工完成此项任务多用10天,且甲队单独施工45天和乙队单独施工30天的工作量相同.
(1)甲、乙两队单独完成此项任务各需多少天?
(2)若甲、乙两队共同工作了3天后,乙队因设备检修停止施工,由甲队继续施工,为了不影响工程进度,甲队的工作效率提高到原来的2倍,要使甲队总的工作量不少于乙队的工作量的2倍,那么甲队至少再单独施工多少天?
查看答案和解析>>
科目: 来源: 题型:
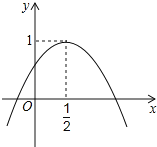
【题目】如图,二次函数y=ax2+bx+c的图象与y轴正半轴相交,其顶点坐标为(![]() ,1),下列结论:其中正确的个数是( )
,1),下列结论:其中正确的个数是( )
①a<0;
②b<0;
③c<0;
④![]() ;
;
⑤a+b+c<0.
A.1 个B.2 个C.3 个D.4 个
查看答案和解析>>
科目: 来源: 题型:
【题目】“构造图形解题”,它的应用十分广泛,特别是有些技巧性很强的题目,如果不能发现题目中所隐含的几何意义,而用通常的代数方法去思考,经常让我们手足无措,难以下手,这时,如果能转换思维,发现题目中隐含的几何条件,通过构造适合的几何图形,将会得到事半功倍的效果,下面介绍两则实例:
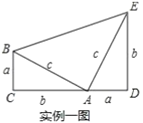
实例一:1876年,美国总统伽非尔德利用实例一图证明了勾股定理:由![]() 四边形
四边形![]() 得
得![]() ,化简得:
,化简得:![]() .
.
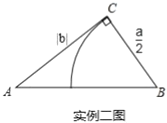
实例二:欧几里得的《几何原本》记载,关于![]() 的方程
的方程![]() 的图解法是:画
的图解法是:画![]() ,使
,使![]() ,
,![]() ,
,![]() ,再在斜边
,再在斜边![]() 上截取
上截取![]() ,则
,则![]() 的长就是该方程的一个正根(如实例二图).
的长就是该方程的一个正根(如实例二图).
根据以上阅读材料回答下面的问题:
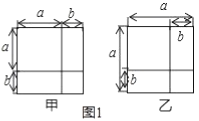
(1)如图1,请利用图形中面积的等量关系,写出甲图要证明的数学公式是 ,乙图要证明的数学公式是 ,体现的数学思想是 ;
(2)如图2,按照实例二的方式构造![]() ,连接
,连接![]() ,请用含字母
,请用含字母![]() 、
、![]() 的代数式表示
的代数式表示![]() 的长,
的长,![]() 的表达式能和已学的什么知识相联系;
的表达式能和已学的什么知识相联系;
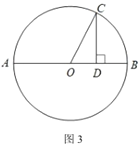
(3)如图3,已知![]() ,
,![]() 为直径,点
为直径,点![]() 为圆上一点,过点
为圆上一点,过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() ,设
,设![]() ,
,![]() ,求证:
,求证:![]() .
.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com