
科目: 来源: 题型:
【题目】已知抛物线![]() 的图象与
的图象与![]() 轴交于
轴交于![]() 和
和![]() 两点(点
两点(点![]() 在点
在点![]() 的左边),点
的左边),点![]() 为抛物线的顶点.
为抛物线的顶点.
(1)求抛物线的函数解析式;
(2)画出此二次函数的大致图像;
(3)点![]() 为线段
为线段![]() 上一点(点
上一点(点![]() 不与点
不与点![]() 、
、![]() 重合),过点
重合),过点![]() 作
作![]() 轴的垂线,与抛物线交于点
轴的垂线,与抛物线交于点![]() ,过点
,过点![]() 作
作![]() 交抛物线于点
交抛物线于点![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() .若点
.若点![]() 在点
在点![]() 左边,求当矩形
左边,求当矩形![]() 的周长最大时点
的周长最大时点![]() 的横坐标.
的横坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】若一个三位数两个数位上数字的和等于另一个数位上的数字,则称这个三位数为“均衡三位数”.现从1,2,3,4,5这5个数字中任取三个数字,组成无重复数字且百位数字、十位数字、个位数字依次增大的三位数.
(1)请列举出所有可能得到的三位数;
(2)小明和小亮玩一个游戏,游戏规则如下:若(1)中组成的三位数是“均衡三位数”,则小明胜;否则小亮胜.这个游戏公平吗?说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】现有一笔直的公路连接![]() 、
、![]() 两地,甲车从
两地,甲车从![]() 地驶往
地驶往![]() 地,速度为每小时60千米,同时乙车从
地,速度为每小时60千米,同时乙车从![]() 地驶往
地驶往![]() 地,速度为每小时80千米.途中甲车发生故障,于是停车修理了2.5小时,修好后立即开车驶往
地,速度为每小时80千米.途中甲车发生故障,于是停车修理了2.5小时,修好后立即开车驶往![]() 地.设甲车行驶的时间为
地.设甲车行驶的时间为![]() ,两车之间的距离为
,两车之间的距离为![]() .已知
.已知![]() 与
与![]() 的函数关系的部分图像如图所示.
的函数关系的部分图像如图所示.
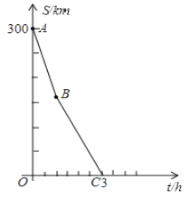
(1)直接写出![]() 点的实际意义.
点的实际意义.
(2)问:甲车出发几小时后发生故障?
(3)将![]() 与
与![]() 的函数图象补充完整.(请对画出的图象用数据作适当的标注)
的函数图象补充完整.(请对画出的图象用数据作适当的标注)
查看答案和解析>>
科目: 来源: 题型:
【题目】数学活动课上,老师和学生一起去测量学校升旗台上旗杆AB的高度,如图,老师测得升旗台前斜坡FC的坡比为iFC=1:10(即EF:CE=1:10),学生小明站在离升旗台水平距离为35m(即CE=35m)处的C点,测得旗杆顶端B的仰角为α,已知tanα=![]() ,升旗台高AF=1m,小明身高CD=1.6m,请帮小明计算出旗杆AB的高度.
,升旗台高AF=1m,小明身高CD=1.6m,请帮小明计算出旗杆AB的高度.
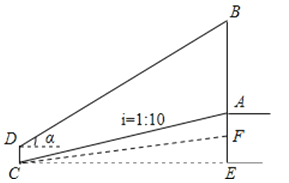
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系xOy中,已知P(x1,y1)Q(x2,y2),定义P、Q两点的横坐标之差的绝对值与纵坐标之差的绝对值的和为P、Q两点的直角距离,记作d(P,Q).即d(P,Q)=|x2﹣x1|+|y2﹣y1|
如图1,在平面直角坐标系xOy中,A(1,4),B(5,2),则d(A,B)=|5﹣1|+|2﹣4|=6.
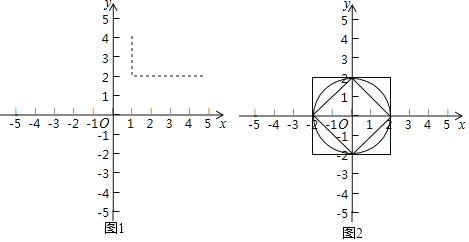
(1)如图2,已知以下三个图形:
①以原点为圆心,2为半径的圆;
②以原点为中心,4为边长,且各边分别与坐标轴垂直的正方形;
③以原点为中心,对角线分别在两条坐标轴上,对角线长为4的正方形.
点P是上面某个图形上的一个动点,且满足d(O,P)=2总成立.写出符合题意的图形对应的序号 .
(2)若直线y=k(x+3)上存在点P使得d(O,P)=2,求k的取值范围.
(3)在平面直角坐标系xOy中,P为动点,且d(O,P)=3,⊙M圆心为M(t,0),半径为1.若⊙M上存在点N使得PN=1,求t的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知梯形ABCD中,AD∥BC,AB=AC,E是边BC上的点,且∠AED=∠CAD,DE交AC于点F.
(1)求证:△ABE∽△DAF;
(2)当ACFC=AEEC时,求证:AD=BE.

查看答案和解析>>
科目: 来源: 题型:
【题目】费尔兹奖是国际上享有崇高荣誉的一个数学奖项,每4年评选一次,在国际数学家大会上颁给有卓越贡献的年龄不超过40岁的年轻数学家,美籍华人丘成桐1982年获得费尔兹奖.为了让学生了解费尔兹奖得主的年龄情况,我们查取了截止到2018年60名费尔兹奖得主获奖时的年龄数据,并对数据进行整理、描述和分析.下面给出了部分信息.
a.截止到2018年费尔兹奖得主获奖时的年龄数据的频数分布直方图如图1(数据分成5组,各组是28≤x<31,31≤x<34,34≤x<37,37≤x<40,x≥40):
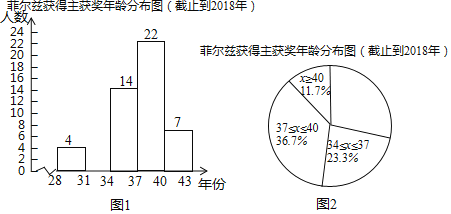
b.如图2,在a的基础上,画出扇形统计图;
c.截止到2018年费尔兹奖得主获奖时的年龄在34≤x<37这一组的数据是:
36 | 35 | 34 | 35 | 35 | 34 | 34 | 35 | 36 | 36 | 36 | 36 | 34 | 35 |
d.截止到2018年时费尔兹奖得主获奖时的年龄的平均数、中位数、众数如下:
年份 | 平均数 | 中位数 | 众数 |
截止到2018 | 35.58 | m | 37,38 |
根据以上信息,回答下列问题:
(1)依据题意,补全频数直方图;
(2)31≤x<34这组的圆心角度数是度,并补全扇形统计图;
(3)统计表中中位数m的值是;
(4)根据以上统计图表试描述费尔兹奖得主获奖时的年龄分布特征.
查看答案和解析>>
科目: 来源: 题型:
【题目】下面是小明设计的“作三角形的高线”的尺规作图过程.
已知:△ABC.
求作:BC边上的高线.
作法:如图,
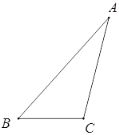
①以点C为圆心,CA为半径画弧;
②以点B为圆心,BA为半径画弧,两弧相交于点D;
③连接AD,交BC的延长线于点E.
所以线段AE就是所求作的BC边上的高线.
根据小明设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面证明.
证明:∵CA=CD,
∴点C在线段AD的垂直平分线上( ) (填推理的依据).
∵ = ,
∴点B在线段AD的垂直平分线上.
∴ BC是线段AD的垂直平分线.
∴AD⊥BC.
∴AE就是BC边上的高线.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线y=ax2﹣2ax+c(a<0)的图象过点A(3,m).
(1)当a=﹣1,m=0时,求抛物线的顶点坐标_____;
(2)如图,直线l:y=kx+c(k<0)交抛物线于B,C两点,点Q(x,y)是抛物线上点B,C之间的一个动点,作QD⊥x轴交直线l于点D,作QE⊥y轴于点E,连接DE.设∠QED=β,当2≤x≤4时,β恰好满足30°≤β≤60°,a=_____.

查看答案和解析>>
科目: 来源: 题型:
【题目】甲、乙两运动员在长为100m的直道AB(A,B为直道两端点)上进行匀速往返跑训练,两人同时从A点起跑,到达B点后,立即转身跑向A点,到达A点后,又立即转身跑向B点,若甲跑步的速度为5m/s,乙跑步的速度为4m/s,则起跑后2分钟内,两人相遇的次数为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com