
科目: 来源: 题型:
【题目】如图(1),已知点G在正方形ABCD的对角线AC上,GE⊥BC,垂足为点E,GF⊥CD,垂足为点F.
(1)证明与推断:
①求证:四边形CEGF是正方形;
②推断:![]() 的值为 :
的值为 :
(2)探究与证明:
将正方形CEGF绕点C顺时针方向旋转α角(0°<α<45°),如图(2)所示,试探究线段AG与BE之间的数量关系,并说明理由:
(3)拓展与运用:
正方形CEGF在旋转过程中,当B,E,F三点在一条直线上时,如图(3)所示,延长CG交AD于点H.若AG=6,GH=2![]() ,则BC= .
,则BC= .

查看答案和解析>>
科目: 来源: 题型:
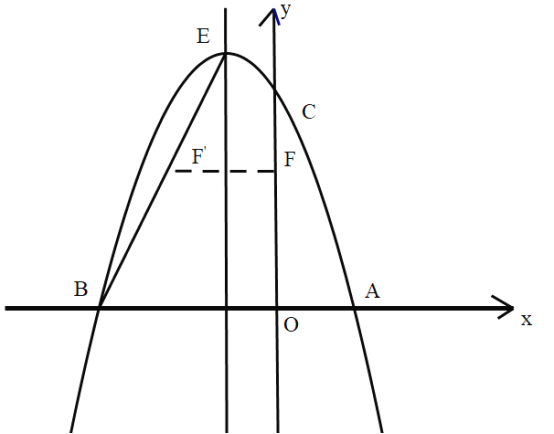
【题目】如图,二次函数![]() 的图像与
的图像与![]() 轴交于
轴交于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,直线l是抛物线的对称轴,
,直线l是抛物线的对称轴,![]() 是抛物线的顶点.
是抛物线的顶点.
(1)求抛物线的解析式及顶点![]() 的坐标;
的坐标;
(2)如图,连接![]() ,线段
,线段![]() 上的点
上的点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() 恰好在线段
恰好在线段![]() 上,求点
上,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】“普洱茶”是云南有名的特产,某网店专门销售某种品牌的普洱茶,成本为30元/盒,每天销售![]() (件)与销售单价
(件)与销售单价![]() (元)之间存在一次函数关系,如图所示.
(元)之间存在一次函数关系,如图所示.
(1)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)如果规定每天该种普洱茶的销售量不低于240盒,该网店店主热心公益事业,决定从每天的销售利润中捐出500元给扶贫基金会,当销售单价为多少元时,每天获取的净利润最大,最大净利润是多少?(注:净利润=总利润-捐款)
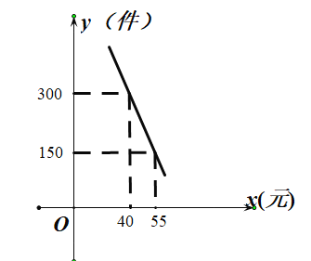
查看答案和解析>>
科目: 来源: 题型:
【题目】某学校举行“青春心向党建功新时代”演讲比赛活动,准备购买甲、乙两种奖品,小昆发现用480元购买甲种奖品的数目恰好与用360元购买乙种奖品的数目相等,已知甲种奖品的单价比乙种奖品的单价多10元.
(1)求甲、乙两种奖品的单价各是多少元?
(2)如果需要购买甲乙两种奖品共100个,且甲种奖品的数目不低于乙种奖品数目的2倍,问购买多少个甲种奖品,才使得总购买费用最少?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,有四张正面标有数字![]() ,背面颜色一样的卡片,正面朝下放在桌面上,小红从中随机抽取一张卡片记下数字,再从余下的卡片中随机抽取一张卡片记下数字.
,背面颜色一样的卡片,正面朝下放在桌面上,小红从中随机抽取一张卡片记下数字,再从余下的卡片中随机抽取一张卡片记下数字.
(1)第一次抽到数字2的卡片的概率是 ;
(2)设第一次抽到的数字为![]() ,第二次抽到的数字为
,第二次抽到的数字为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,请用树状图或列表法求点
,请用树状图或列表法求点![]() 在第三象限的概率.
在第三象限的概率.
![]()
![]()
![]()
![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】4月23日为世界阅读日,为响应党中央“倡导全民阅读,建设书香会”的号召,某校团委组织了一次全校学生参加的“读书活动”大赛为了解本次赛的成绩,校团委随机抽取了部分学生的成绩(成绩![]() 取整数,总分100分)作为本进行统计,制成如下不完整的统计图表(频数频率分布表和频数分布直方图):
取整数,总分100分)作为本进行统计,制成如下不完整的统计图表(频数频率分布表和频数分布直方图):
成绩 | 频数(人) | 频率 |
| 10 | 0.05 |
| 30 | 0.15 |
| 40 |
|
|
| 0.35 |
| 50 | 0.25 |
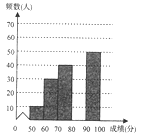
根据所给信息,解答下列问题:
(1)抽取的样本容量是 ;![]() ,
,![]() ;
;
(2)补全频数分布直方图;这200名学生成绩的中位数会落在 分数段;
(3)全校有1200名学生参加比赛,若得分为90分及以上为优秀,请你估计全校参加比赛成绩优秀的学生人数.
查看答案和解析>>
科目: 来源: 题型:
【题目】我们做如下的规定:如果一个三角形在运动变化时保持形状和大小不变,则把这样的三角形称为三角形板.
把两块边长为4的等边三角形板![]() 和
和![]() 叠放在一起,使三角形板
叠放在一起,使三角形板![]() 的顶点
的顶点![]() 与三角形板
与三角形板![]() 的AC边中点
的AC边中点![]() 重合,把三角形板
重合,把三角形板![]() 固定不动,让三角形板
固定不动,让三角形板![]() 绕点
绕点![]() 旋转,设射线
旋转,设射线![]() 与射线
与射线![]() 相交于点M,射线
相交于点M,射线![]() 与线段
与线段![]() 相交于点N.
相交于点N.
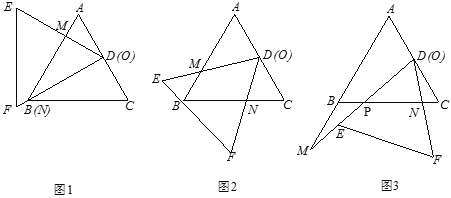
(1)如图1,当射线![]() 经过点
经过点![]() ,即点N与点
,即点N与点![]() 重合时,易证△ADM∽△CND.此时,AM·CN= .
重合时,易证△ADM∽△CND.此时,AM·CN= .
(2)将三角形板![]() 由图1所示的位置绕点
由图1所示的位置绕点![]() 沿逆时针方向旋转,设旋转角为
沿逆时针方向旋转,设旋转角为![]() .其中
.其中![]() ,问AM·CN的值是否改变?说明你的理由.
,问AM·CN的值是否改变?说明你的理由.
(3)在(2)的条件下,设AM= x,两块三角形板重叠面积为![]() ,求
,求![]() 与
与![]() 的函数关系式.(图2,图3供解题用)
的函数关系式.(图2,图3供解题用)
查看答案和解析>>
科目: 来源: 题型:
【题目】研究发现,二次函数![]() (
(![]() )图象上任何一点到定点(0,
)图象上任何一点到定点(0,![]() )和到定直线
)和到定直线![]() 的距离相等.我们把定点(0,
的距离相等.我们把定点(0,![]() )叫做抛物线
)叫做抛物线![]() 的焦点,定直线
的焦点,定直线![]() 叫做抛物线
叫做抛物线![]() 的准线.
的准线.
(1)写出函数![]() 图象的焦点坐标和准线方程;
图象的焦点坐标和准线方程;
(2)等边三角形OAB的三个顶点都在二次函数![]() 图象上,O为坐标原点,求等边三角形的边长;
图象上,O为坐标原点,求等边三角形的边长;
(3)M为抛物线![]() 上的一个动点,F为抛物线
上的一个动点,F为抛物线![]() 的焦点,P(1,3)为定点,求MP+MF的最小值.
的焦点,P(1,3)为定点,求MP+MF的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com