
科目: 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°(AC>BC),用尺规作图的方法作线段AD,保留作图痕迹如图所示,认真观察作图痕迹,若CD=4,BD=5,则AC的长为( )
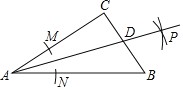
A.6B.9C.12D.15
查看答案和解析>>
科目: 来源: 题型:
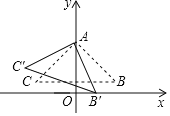
【题目】如图,在Rt△ABC中,∠CAB=90°,AB=AC,点A在y轴上,BC∥x轴,点B![]() .将△ABC绕点A顺时针旋转的△AB′C′,当点B′落在x轴的正半轴上时,点C′的坐标为( )
.将△ABC绕点A顺时针旋转的△AB′C′,当点B′落在x轴的正半轴上时,点C′的坐标为( )
A.(﹣![]() ,
,![]() ﹣1)B.(﹣
﹣1)B.(﹣![]() ,
,![]() ﹣1)
﹣1)
C.(﹣![]() ,
,![]() +1)D.(﹣
+1)D.(﹣![]() ,
,![]() ﹣1)
﹣1)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平行四边形ABCD中AC,BD相交于点O,点E是OA的中点,连接BE并延长AD于点F,已知△AEF的面积=1,则平行四边形ABCD的面积是( )
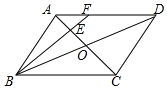
A.24B.18C.12D.9
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系xOy中,对于任意两点P1(x1,y1),P2(x2,y2),如果![]() ,则称P1与P2互为“d-距点”.例如:点P1(3,6),点P2(1,7),由d=|3-1|+|6-7|=3,可得点P1与P2互为“3-距点”.
,则称P1与P2互为“d-距点”.例如:点P1(3,6),点P2(1,7),由d=|3-1|+|6-7|=3,可得点P1与P2互为“3-距点”.
(1)在点D(-2,-2),E(5,-1),F(0,4)中,原点O的“4-距点"是____(填字母);
(2)已知点A(2,1),点B(0,b),过点B作平行于x轴的直线l.
①当b=3时,直线l上点A的“2-距点"的坐标为_______;
②若直线l上存在点A的2-距点”,求b的取值范围:
(3)已知点M(1,2),N(3,2),C(m,0),⊙C的半径为![]() ,若在线段MN上存在点P,在⊙C上存在点Q,使得点P与点Q互为“5-距点",直接写出m的取值范围.
,若在线段MN上存在点P,在⊙C上存在点Q,使得点P与点Q互为“5-距点",直接写出m的取值范围.
查看答案和解析>>
科目: 来源: 题型:
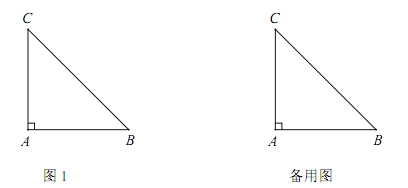
【题目】如图,在△ABC中,∠BAC=90°,AB=AC,点P为线段AC上一点,点Q在线段AB的延长线上,CP=BQ,连接PQ交BC于点D,点P关于BC的对称点为E,连接AE.
(1)依题意补全图1;
(2)求证:D是PQ的中点;
(3)用等式表示AE和PQ的数量关系,并证明.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线![]() 与y轴交于点A,它的顶点为点B.
与y轴交于点A,它的顶点为点B.
(1)点A的坐标为______,点B的坐标为______(用m表示);
(2)已知点M(-6,4),点N(3,4),若抛物线与线段MN恰有一个公共点,结合函数图象,求m的取值范围.
查看答案和解析>>
科目: 来源: 题型:
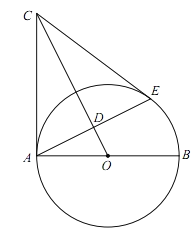
【题目】已知:如图,AB是⊙O的直径,点C是过点A的⊙O的切线上一点,连接OC,过点A作OC的垂线交OC于点D,交⊙O于点E,连接CE.
(1)求证:CE与⊙O相切;
(2)连结BD并延长交AC于点F,若OA=5,sin∠BAE=![]() ,求AF的长.
,求AF的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系xOy中,直线y=2x+b与双曲线![]() 交于A,B两点.P是线段AB上一点(不与点A,点B重合),过点P作平行于x轴的直线交双曲线
交于A,B两点.P是线段AB上一点(不与点A,点B重合),过点P作平行于x轴的直线交双曲线![]() 于点M,过点P作平行于y轴的直线交双曲线
于点M,过点P作平行于y轴的直线交双曲线![]() 于点N.
于点N.
(1)当点A的横坐标为1时,求b的值:
(2)在(1)的条件下,设P点的横坐标为m,
①若m=-1,判断PM与PN的数量关系,并说明理由;
②若PM<PN,结合函数图象,直接写出m的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】2018年9月17日世界人工智能大会在.上海召开,人工智能的变革力在教育、制造等领域加速落地.在某市举办的一次中学生机器人足球赛中,有四个代表队进入决赛,决赛中,每个队分别与其它三个队进行主客场比赛各一场(即每个队要进行6场比赛),以下是积分表的一-部分.
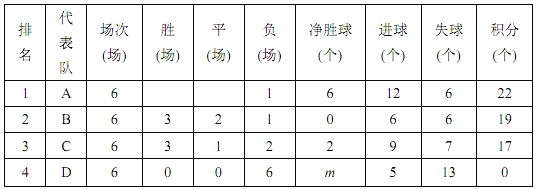
(说明:积分=胜场积分十平场积分+负场积分)
(1)D代表队的净胜球数m=______;
(2)本次决赛中,胜一场积______分,平一场积______分,负一场积_______分;
(3)此次竞赛的奖金分配方案为:进入决赛的每支代表队都可以获得参赛奖金6000元;另外,在决赛期间,每胜一场可以再获得奖金2000元,每平一场再获得奖金1000元.请根据表格提供的信息,求出冠军A队一共能获得多少奖金.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com