
科目: 来源: 题型:
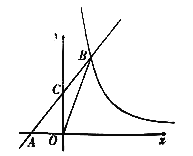
【题目】如图,在平面直角坐标系xOy中,直线y=kx+b(k≠0)与轴交于点A(-2.0),与反比例函数y=![]() (m≠0)的图象交于点B(2,n),连接BO,若S△AOB=4.
(m≠0)的图象交于点B(2,n),连接BO,若S△AOB=4.
(1)求反比例函数和一次函数的表达式:
(2)若直线AB与y轴的交点为C.求△OCB的面积
(3)根据图象,直接写出当x>0时,不等式![]() >kx+b的解集.
>kx+b的解集.
查看答案和解析>>
科目: 来源: 题型:
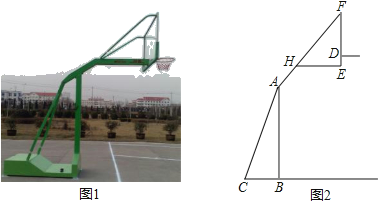
【题目】如图1,2分别是某款篮球架的实物图与示意图,AB⊥BC于点B,底座BC=1.3米,底座BC与支架AC所成的角∠ACB=60°,点H在支架AF上,篮板底部支架EH∥BC.EF⊥EH于点E,已知AH=![]() 米,HF=
米,HF=![]() 米,HE=1米.
米,HE=1米.
(1)求篮板底部支架HE与支架AF所成的∠FHE的度数.
(2)求篮板底部点E到地面的距离,(精确到0.01米)(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目: 来源: 题型:
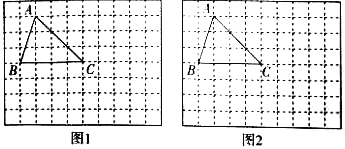
【题目】如图,在由边长为1个单位长度的小正方形组成的网格图中有格点△ABC(注:顶点在网格线交点处的三角形叫做格点三角形).只用没有刻度的直尺,按如下要求画图,
(1)以点C为位似中心,在如图中作△DEC∽ABC,且相似比为1:2;
(2)若点B为原点,点C(4,0),请在如图中画出平面直角坐标系,作出△ABC的外心,并直接写出△ABC的外心的坐标
查看答案和解析>>
科目: 来源: 题型:
【题目】《孙子算经》是中国古代重要的数学著作,其中记载:“今有甲、乙二人,持钱各不知数.甲得乙中半,可满四十八;乙得甲太半,亦满四十八。问甲、乙二人原持钱各几何?”译文:“甲,乙两人各有若干钱,如果甲得到乙所有钱的一半,那么甲共有钱48文,如果乙得到甲所有钱的![]() ,那么乙也共有钱48文,问甲、乙二人原来各有多少钱?”
,那么乙也共有钱48文,问甲、乙二人原来各有多少钱?”
查看答案和解析>>
科目: 来源: 题型:
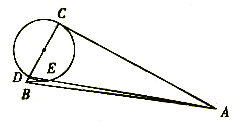
【题目】在Rt△ABC中,∠ACB=90°.AC=8,BC=3,点D是BC边上动点,连接AD交以CD为直径的圆于点E,则线段BE长度的最小值为( )
A.1B.![]() C.
C. ![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】如图甲,在四边形ABCD中,AD//BC,∠C=90°动点P从点C出发沿线段CD向点D运动.到达点D即停止,若E、F分别是AP、BP的中点,设CP=x,△PEF的面积为y,且y与x之间的函数关系的图象如图乙所示,则线段AB长为( )
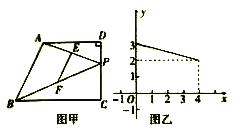
A.2![]() B.2
B.2![]() C.2
C.2![]() D.2
D.2![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,平行四边形ABCD中,∠BDC=30°,DC=4,AE⊥BD于E,CF⊥BD于F,且E、F恰好是BD的三等分点,AE、CF的延长线分别交DC、AB于N、M点,那么四边形MENF的面积是( )

A.![]() B.
B.![]() C.2
C.2![]() D.2
D.2![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】小明对九(1)、九(2)班(人数都为50人)参加“阳光体育”的情况进行了调查,统计结果如图所示.下列说法中正确的是( )
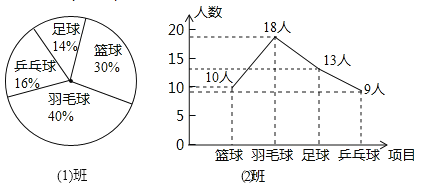
A.喜欢乒乓球的人数(1)班比(2)班多B.喜欢足球的人数(1)班比(2)班多
C.喜欢羽毛球的人数(1)班比(2)班多D.喜欢篮球的人数(2)班比(1)班多
查看答案和解析>>
科目: 来源: 题型:
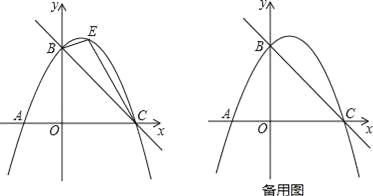
【题目】如图,直线y=﹣![]() x+3与x轴交于点C,与y轴交于点B,抛物线y=ax2+
x+3与x轴交于点C,与y轴交于点B,抛物线y=ax2+![]() x+c经过B、C两点.
x+c经过B、C两点.
(1)求抛物线的解析式;
(2)如图,点E是直线BC上方抛物线上的一动点,当△BEC面积最大时,请求出点E的坐标和△BEC面积的最大值?
(3)在(2)的结论下,过点E作y轴的平行线交直线BC于点M,连接AM,点Q是抛物线对称轴上的动点,在抛物线上是否存在点P,使得以P、Q、A、M为顶点的四边形是平行四边形?如果存在,请直接写出点P的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】为了美化环境,建设宜居成都,我市准备在一个广场上种植甲、乙两种花卉.经市场调查,甲种花卉的种植费用![]() (元)与种植面积
(元)与种植面积![]() 之间的函数关系如图所示,乙种花卉的种植费用为每平方米100元.
之间的函数关系如图所示,乙种花卉的种植费用为每平方米100元.
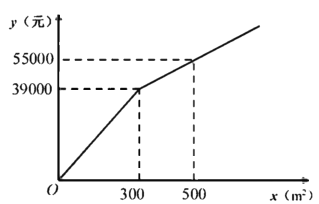
(1)直接写出当![]() 和
和![]() 时,
时,![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)广场上甲、乙两种花卉的种植面积共![]() ,若甲种花卉的种植面积不少于
,若甲种花卉的种植面积不少于![]() ,且不超过乙种花卉种植面积的2倍,那么应该怎样分配甲、乙两种花卉的种植面积才能使种植费用最少?最少总费用为多少元?
,且不超过乙种花卉种植面积的2倍,那么应该怎样分配甲、乙两种花卉的种植面积才能使种植费用最少?最少总费用为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com