
科目: 来源: 题型:
【题目】重庆一中开展了“爱生活爱运动”的活动,以鼓励学生积极参与体育锻炼.为了解学生每周体育锻炼时间,学校在活动之前对八年级同学进行了抽样调査,并根据调査结果将学生每周的体育锻炼时间分为3小时、4小时、5小时、6小时、7小时共五种情况.小明根据调查结构制作了如图两幅统计图,请你结合图中所给信息解答下列问题:
(整理数据)
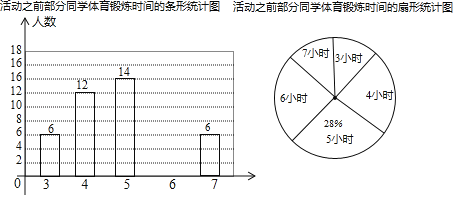
“爱生活爱运动”的活动结束之后,再次抽查这部分学生的体育锻炼时间:
一周体育锻炼时间(小时) | 3 | 4 | 5 | 6 | 7 |
人数 | 3 | 5 | 15 | a | 10 |
活动之后部分学生体育锻炼时间的统计表
(分析数据)
平均数 | 中位数 | 众数 | |
活动之前锻炼时间(小时) | 5 | 5 | 5 |
活动之后锻炼时间(小时) | 5.52 | b | c |
请根据调查信息
(1)补全条形统计图,并计算a= ,b= 小时,c= 小时;
(2)小亮同学在活动之前与活动之后的这两次调查中,体育锻炼时间均为5小时,根据体育锻炼时间由多到少进行排名统计,请问他在被调查同学中体育锻炼时间排名靠前的是 (填“活动之前”或“活动之后”),理由是 ;
(3)已知八年级共2200名学生,请估算全年级学生在活动结束后,每周体育锻炼时间至少有6小时的学生人数有多少人?
查看答案和解析>>
科目: 来源: 题型:
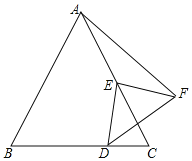
【题目】如图:△ABC是等边三角形,AB=12,E是AC中点,D是直线BC上一动点,线段ED绕点E逆时针旋转90°,得线段EF,当点D运动时,则线段AF的最小值为_____.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在扇形AOB中,∠AOB=90°,正方形CDEF的顶点C是![]() 的中点,点D在OB上,点E在OB的延长线上,当正方形CDEF的边长为2
的中点,点D在OB上,点E在OB的延长线上,当正方形CDEF的边长为2![]() 时,阴影部分的面积为________
时,阴影部分的面积为________
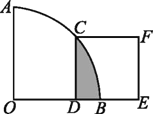
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,正方形OABC的边长为2,以O为圆心,EF为直径的半圆经过点A,连接AE、CF相交于点P.将正方形OABC从OA与OF重合的位置开始,绕着点O逆时针旋转90°的过程中,线段OP的最小值为_____.
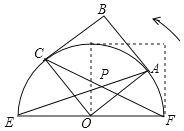
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在一单位为1的方格纸上,![]() ,
,![]() ,
,![]() …,都是斜边在
…,都是斜边在![]() 轴上,斜边长分别为2,4,6,…的等腰直角三角形,若
轴上,斜边长分别为2,4,6,…的等腰直角三角形,若![]() 的顶点坐标分别为
的顶点坐标分别为![]() ,
,![]() ,
,![]() ,则依图中所示规律,
,则依图中所示规律,![]() 的坐标为( )
的坐标为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】问题背景:我们学习等边三角形时得到直角三角形的一个性质:在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.即:如图1,在Rt△ABC中,∠ACB=90°,∠ABC=30°,则:AC=![]() AB.
AB.

探究结论:小明同学对以上结论作了进一步研究.
(1)如图1,连接AB边上中线CE,由于CE=![]() AB,易得结论:①△ACE为等边三角形;②BE与CE之间的数量关系为 .
AB,易得结论:①△ACE为等边三角形;②BE与CE之间的数量关系为 .
(2)如图2,点D是边CB上任意一点,连接AD,作等边△ADE,且点E在∠ACB的内部,连接BE.试探究线段BE与DE之间的数量关系,写出你的猜想并加以证明.
(3)当点D为边CB延长线上任意一点时,在(2)条件的基础上,线段BE与DE之间存在怎样的数量关系?请直接写出你的结论 .
拓展应用:如图3,在平面直角坐标系xOy中,点A的坐标为(﹣![]() ,1),点B是x轴正半轴上的一动点,以AB为边作等边△ABC,当C点在第一象限内,且B(2,0)时,求C点的坐标.
,1),点B是x轴正半轴上的一动点,以AB为边作等边△ABC,当C点在第一象限内,且B(2,0)时,求C点的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】某数学兴趣小组在探究函数y=|x2-4x+3|的图象和性质时,经历以下几个学习过程:
(1)列表(完成以下表格)
x | … | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | … |
y1=x2-4x+3 | … | 15 | 8 | 0 | 0 | 3 | 15 | … | |||
y=|x2-4x+3| | … | 15 | 8 | 0 | 0 | 3 | 15 | … |
(2)描点并画出函数图象草图(在备用图1中描点并画图)

(3)根据图象完成以下问题
(ⅰ)观察图象
函数y=|x2-4x+3|的图象可由函数y1=x2-4x+3的图象如何变化得到?
答:______.
(ⅱ)数学小组探究发现直线y=8与函数y=|x2-4x+3|的图象交于点E、F,E(-1,8),F(5,8),则不等式|x2-4x+3|>8的解集是______;
(ⅲ)设函数y=|x2-4x+3|的图象与x轴交于A、B两点(B位于A的右侧),与y轴交于点C.
①求直线BC的解析式;
②探究应用:将直线BC沿y轴平移m个单位后与函数y=|x2-4x+3|的图象恰好有3个交点,求此时m的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AO⊥BC于点O,OE⊥AB于点E,以点O为圆心,OE为半径作半圆,交AO于点F.
(1)求证:AC是⊙O的切线;
(2)若点F是OA的中点,OE=3,求图中阴影部分的面积;
(3)在(2)的条件下,点P是BC边上的动点,当PE+PF取最小值时,直接写出BP的长.

查看答案和解析>>
科目: 来源: 题型:
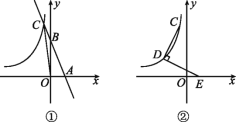
【题目】如图①,直线y=-2x+4交x轴、y轴于A,B两点,交双曲线y=![]() (x<0)于C点,△OAC的面积为6.
(x<0)于C点,△OAC的面积为6.
(1)求双曲线的解析式;
(2)如图②,D为双曲线y=![]() (x<0)上一点,连接CD,将线段CD绕点D顺时针旋转90°得线段DE,点E恰好落在x轴上,求点E的坐标.
(x<0)上一点,连接CD,将线段CD绕点D顺时针旋转90°得线段DE,点E恰好落在x轴上,求点E的坐标.
查看答案和解析>>
科目: 来源: 题型:
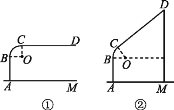
【题目】如图是一个桌面会议话筒示意图,中间BC部分是一段可弯曲的软管,在弯曲时可形成一段圆弧,设圆弧所在圆的圆心为O,线段AB,CD均与圆弧相切,点B,C分别为切点,已知AB的长10 cm,CD的长为25.2 cm.
(1)如图①,若话筒弯曲后CD与桌面AM平行,此时CD距离桌面14 cm,求弧BC的长度(结果保留π);
(2)如图②,若话筒弯曲后弧BC所对的圆心角度数为60°,求话筒顶端D到桌面AM的距离(结果保留一位小数).(参考数据:![]() ≈1.73)
≈1.73)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com