
科目: 来源: 题型:
【题目】如图,抛物线![]() 经过点B(3,0),C(0,-2),直线L:
经过点B(3,0),C(0,-2),直线L:![]() 交y轴于点E,且与抛物线交于A,D两点,P为抛物线上一动点(不与A重合).
交y轴于点E,且与抛物线交于A,D两点,P为抛物线上一动点(不与A重合).
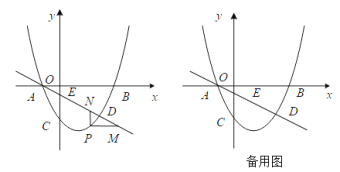
(1)求抛物线的解析式.
(2)当点P在直线L下方时,过点P作PM∥x轴交L于点M,PN∥y轴交L于点N,求PM+PN的最大值.
(3)设F为直线L上的点,以E,C,P,F为顶点的四边形能否构成平行四边形?若能,求出点F的坐标;若不能,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】问题背景:如图1,等腰△ABC中,AB=AC,∠BAC=120°,作AD⊥BC于点D,则D为BC的中点,∠BAD=![]() ∠BAC=60°,于是
∠BAC=60°,于是![]() =
= ![]() =
=![]() ;
;
迁移应用:如图2,△ABC和△ADE都是等腰三角形,∠BAC=∠DAE=120°,D,E,C三点在同一条直线上,连接BD.
①求证:△ADB≌△AEC;
②请直接写出线段AD,BD,CD之间的等量关系式;
拓展延伸:如图3,在菱形ABCD中,∠ABC=120°,在∠ABC内作射线BM,作点C关于BM的对称点E,连接AE并延长交BM于点F,连接CE,CF.
①证明△CEF是等边三角形;
②若AE=5,CE=2,求BF的长.
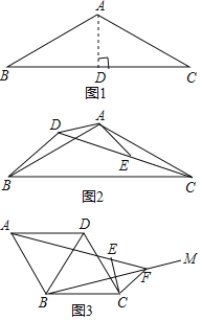
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,AB为⊙O直径,C、D为⊙O上不同于A、B的两点,∠ABD=2∠BAC,连接CD.过点C作CE⊥DB,垂足为E,直线AB与CE相交于F点.
(1)求证:CF为⊙O的切线;
(2)当BF=5,![]() 时,求BD的长.
时,求BD的长.

查看答案和解析>>
科目: 来源: 题型:
【题目】某经销商销售一种成本价为10元/kg的商品,已知销售价不低于成本价,且物价部门规定这种产品的销售价不得高于18元/kg.在销售过程中发现销量y(kg)与售价x(元/kg)之间满足一次函数关系,对应关系如下表所示:

⑴求y与x之间的函数关系式,并写出自变量x的取值范围;
⑵若该经销商想使这种商品获得平均每天168元的利润,求售价应定为多少元/kg?
⑶设销售这种商品每天所获得的利润为W元,求W与x之间的函数关系式;并求出该商品销售单价定为多少元时,才能使经销商所获利润最大?最大利润是多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图 1,将一张矩形纸片 ABCD 沿着对角线 BD 向上折叠,顶点 C 落到点 E 处,BE 交 AD 于点 F.
(1)求证:△BDF 是等腰三角形;
(2)如图 2,过点 D 作 DG∥BE,交 BC 于点 G,连接 FG 交 BD 于点 O.
①判断四边形 BFDG 的形状,并说明理由;
②若 AB=6,AD=8,则 FG 的长为_____.
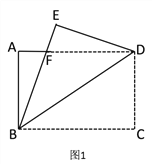

查看答案和解析>>
科目: 来源: 题型:
【题目】我们知道良好的坐姿有利于青少年骨骼生长,有利于身体健康,那么首先要有正确的写字坐姿,身子上半部坐直,头部端正、目视前方,两手放在桌面上,两腿平放,胸膛挺起,理想状态下,如图1所示,将图1中的眼睛记为点A,腹记为点B,笔尖记为点D,且BD与桌沿的交点记为点C
(1)若∠ADB=53°,∠B=60°,求A到BD的距离及C、D两点间的距离(结果精确到1cm).
(2)老师发现小红同学写字姿势不正确,眼睛倾斜至图2的点E,点E正好在CD的垂直平分线上,且∠BDE=60°,于是要求其纠正为正确的姿势.求眼睛所在的位置应上升的距离.(结果精确到1cm)
参考数据:sin53°≈0.80,cos53°≈0.60,.tan53°≈1.33,![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
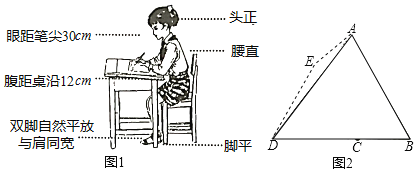
查看答案和解析>>
科目: 来源: 题型:
【题目】十八大以来,某校已举办五届校园艺术节.为了弘扬中华优秀传统文化,每届艺术节上都有一些班级表演“经典诵读”、“民乐演奏”、“歌曲联唱”、“民族舞蹈”等节目.小颖对每届艺术节表演这些节目的班级数进行统计,并绘制了如图所示不完整的折线统计图和扇形统计图.
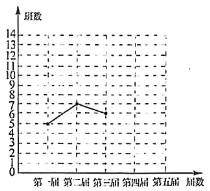
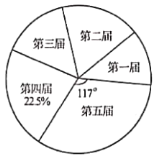
(1)五届艺术节共有________个班级表演这些节日,班数的中位数为________,在扇形统计图中,第四届班级数的扇形圆心角的度数为________;
(2)补全折线统计图;
(3)第六届艺术节,某班决定从这四项艺术形式中任选两项表演(“经典诵读”、“民乐演奏”、“歌曲联唱”、“民族舞蹈”分别用![]() ,
,![]() ,
,![]() ,
,![]() 表示).利用树状图或表格求出该班选择
表示).利用树状图或表格求出该班选择![]() 和
和![]() 两项的概率.
两项的概率.
查看答案和解析>>
科目: 来源: 题型:
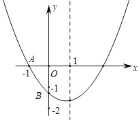
【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(﹣1,0),与y轴的交点B在(0,﹣2)和C(0,﹣1)之间(不包括这两点),对称轴为直线x=1,下列结论:①abc>0;②4a+2b+c>0;③4ac﹣b2<8a;④![]() ;⑤b<c.其中含所有正确结论的选项是_____.
;⑤b<c.其中含所有正确结论的选项是_____.
查看答案和解析>>
科目: 来源: 题型:
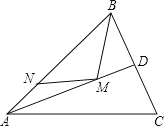
【题目】如图,在锐角△ABC中,AB=5![]() ,∠BAC=45°,∠BAC的平分线交BC于点D,M,N分别是AD,AB上的动点,则BM+MN的最小值是______.
,∠BAC=45°,∠BAC的平分线交BC于点D,M,N分别是AD,AB上的动点,则BM+MN的最小值是______.
查看答案和解析>>
科目: 来源: 题型:
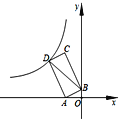
【题目】如图,点A(-2,0),B(0,1),以线段AB为边在第二象限作矩形ABCD,双曲线![]() (k<0)经过点D,连接BD,若四边形OADB的面积为6,则k的值是_____.
(k<0)经过点D,连接BD,若四边形OADB的面积为6,则k的值是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com