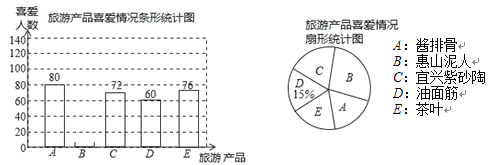
根据以上信息完成下列问题：

（1）请将条形统计图补充完整．

（2）在扇形统计图中，A部分所占的圆心角是 度．

（3）根据调查结果估计这天在所有的游客中最喜爱惠山泥人的约有多少人．

（1）当主持人询问艾热准备奇袭哪位歌手时，艾热透露“希望和男性嗓音去比试”，那周深被奇袭的概率是 ；

（2）7名主打歌手比赛的上场顺序是通过抽签方式进行，若已经知道前4位歌手的上场顺序，还有华晨宇、米希亚、周深不知道，那么华晨宇和周深两位是相邻出场的概率是多少．（请用“画树状图”或“列表”等方法写出分析过程）

【题目】如图，在平面直角坐标系中，点A在第一象限，BA⊥y轴于点B，反比例函数y=（x＞0）的图象与线段AB相交于点C，且C是线段AB的中点，若△OAB的面积为3，则k的值为( )

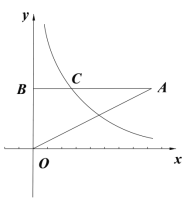
A.B.1C.2D.3

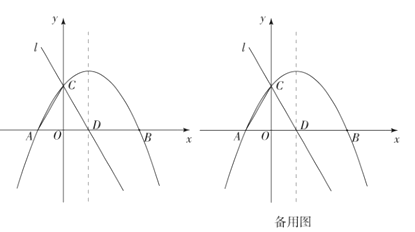
【题目】综合与探究：在平面直角坐标系中，已知抛物线与轴交于，两点(点在点的右侧)，与轴交于点，它的对称轴与轴交于点，直线经过，两点，连接．

（1）求，两点的坐标及直线的函数表达式；

（2）探索直线上是否存在点，使为直角三角形，若存在，求出点的坐标；若不存在，说明理由；

（3）若点是直线上的一个动点，试探究在抛物线上是否存在点：

①使以点，，，为顶点的四边形为菱形，若存在，请直接写出点的坐标；若不存在，说明理由；

②使以点，，，为顶点的四边形为矩形，若存在，请直接写出点的坐标；若不存在，说明理由.

正方形内“奇妙点”及性质探究

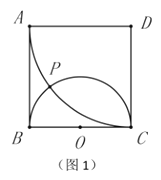
定义：如图1，在正方形中，以为直径作半圆，以为圆心，为半径作，与半圆交于点.我们称点为正方形的一个“奇妙点”．过奇妙点的多条线段与正方形无论是位置关系还是数量关系，都具有不少优美的性质值得探究．

性质探究：如图2，连接并延长交于点，则为半圆的切线．

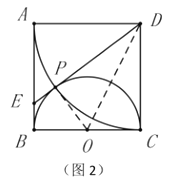
证明：连接．

由作图可知，，

又．

，∴是半圆的切线．

问题解决：

（1）如图3，在图2的基础上，连接.请判断和的数量关系，并说明理由；

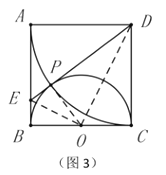
（2）在（1）的条件下，请直接写出线段之间的数量关系；

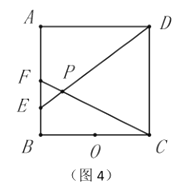
（3）如图4，已知点为正方形的一个“奇妙点”，点为的中点，连接并延长交于点，连接并延长交于点，请写出和的数量关系，并说明理由；

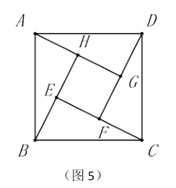
（4）如图5，已知点为正方形的四个“奇妙点”．连接，恰好得到一个特殊的“赵爽弦图”．请根据图形，探究并直接写出一个不全等的几何图形面积之间的数量关系．

【题目】“十三五”以来，山西省共解决372个村、35.8万农村人口的饮水型氟超标问题，让农村群众真正喝上干净水、放心水、安全水．某公司抓住商机，根据市场需求代理，两种型号的净水器，已知每台型净水器比每台型净水器进价多200元，用5万元购进型净水器与用4.5万元购进型净水器的数量相等．

（1）求每台型，型净水器的进价各是多少元？

（2）该公司计划购进，两种型号的净水器共55台进行试销，其中型净水器为台，购买两种净水器的总资金不超过10.8万元．则最多可购进型号净水器多少台？

经统计发现两队5名队员踢毽子的总个数相等，按照比赛规则，两队获得并列第一．学习统计知识后，我们可以通过考查数据中的其它信息作为参考，进行综合评定：

（1）甲、乙两队的优秀率分别为　　　　；

（2）甲队比赛数据的中位数为　　　　个；乙队比赛数据的中位数为　　　　个；

（3）分别计算甲、乙两队比赛数据的方差；

（4）根据以上信息，你认为综合评定哪一个队的成绩好？简述理由．

“整体思想”是中学数学中的一种重要思想，贯穿于中学数学的全过程，比如整体代入，整体换元，整体约减，整体求和，整体构造，…，有些问题若从局部求解，采取各个击破的方式，很难解决，而从全局着眼，整体思考，会使问题化繁为简，化难为易，复杂问题也能迎刃而解．

例：当代数式的值为7时，求代数式的值．

解：因为，所以．

所以．

以上方法是典型的整体代入法．

请根据阅读材料，解决下列问题：

（1）已知，求的值．

（2）我们知道方程的解是，现给出另一个方程，则它的解是　　　　．

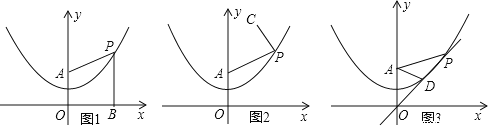
【题目】已知，在平面直角坐标系xOy中，点A的坐标为(0，2)，点P(m，n)是抛物线上的一个动点.

(1)如图1，过动点P作PB⊥x轴，垂足为B，连接PA，请通过测量或计算，比较PA与PB的大小关系：PA_____PB(直接填写“＞”“＜”或“=”，不需解题过程)；

(2)请利用(1)的结论解决下列问题：

①如图2，设C的坐标为(2，5)，连接PC，AP+PC是否存在最小值？如果存在，求点P的坐标；如果不存在，简单说明理由；

②如图3，过动点P和原点O作直线交抛物线于另一点D，若AP=2AD，求直线OP的解析式.

（1）当m＜0时，函数y＝mx2﹣（2m+1）x+2在x＞1时，y随x的增大而减小；

（2）当m＞0时，函数y＝mx2﹣（2m+1）x+2图象截x轴上的线段长度小于2．