
科目: 来源: 题型:
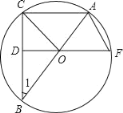
【题目】如图,已知△ABC内接于⊙O,AB是直径,OD⊥BC于点D,延长DO交⊙O于F,连接OC,AF.
(1)求证:△COD≌△BOD;
(2)填空:①当∠1= 时,四边形OCAF是菱形;
②当∠1= 时,AB=2![]() OD.
OD.
查看答案和解析>>
科目: 来源: 题型:
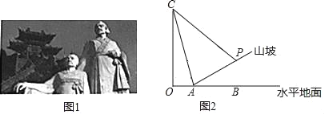
【题目】某游客计划测量这座塑像的高度,(如图1),由于游客无法直接到达塑像底部,因此该游客计划借助坡面高度来测量塑像的高度;如图2,在塑像旁山坡坡脚A处测得塑像头顶C的仰角为75°,当从A处沿坡面行走10米到达P处时,测得塑像头顶C的仰角刚好为45°,已知山坡的坡度i=1:3,且O,A,B在同一直线上,求塑像的高度.(侧倾器高度忽略不计,结果精确到0.1米,参考数据:cos75°≈0.3,tan75°≈3.7,![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】某校学生会发现同学们就餐时剩余饭菜较多,浪费严重,于是准备在校内倡导“光盘行动”,让同学们珍惜粮食,为了让同学们理解这次活动的重要性,校学生会在某天午餐后,随机调查了部分同学这餐饭菜的剩余情况,并将结果统计后绘制成了如图所示的不完整的统计图.
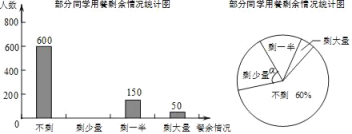
(1)这次被调查的同学共有 人;
(2)补全条形统计图,并在图上标明相应的数据;
(3)扇形统计图中圆心角α= 度;
(4)校学生会通过数据分析,估计这次被调查的所有学生一餐浪费的食物可以供50人食用一餐.据此估算,该校18000名学生一餐浪费的食物可供多少人食用一餐.
查看答案和解析>>
科目: 来源: 题型:
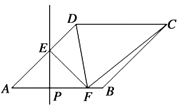
【题目】如图,在菱形ABCD中,∠DAB=45°,AB=4,点P为线段AB上一动点(不与点A重合),过点P作PE⊥AB交射线AD于点E,沿PE将△APE折叠,点A的对称点为点F,连接EF,DF,CF,当△CDF为等腰三角形时,AP的长为________.
查看答案和解析>>
科目: 来源: 题型:
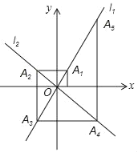
【题目】如图,在平面直角坐标系中,函数y=2x和y=﹣x的图象分别为直线l1,l2,过点(1,0)作x轴的垂线交l1于点A1,过点A1作y轴的垂线交l2于点A2,过点A2作x轴的垂线交l1于点A3,过点A3作y轴的垂线交l2于点A4,…,依次进行下去,则点A2019的坐标为( )
A.(21009,21010)B.(﹣21009,21010)
C.(21009,﹣21010)D.(﹣21009,﹣21010)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,在![]() 中,
中,![]() ,点
,点![]() 为
为![]() 边上的动点,
边上的动点,![]() 交
交![]() 于点
于点![]() .
.
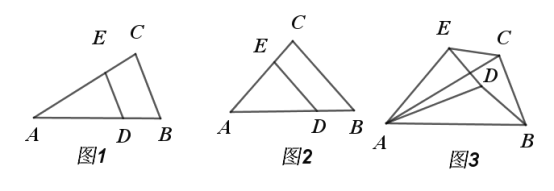
问题发现:(1)如图2,当![]() 时,
时,![]() ;
;![]() 与
与![]() 所在直线相交所成的锐角等于__________.
所在直线相交所成的锐角等于__________.
类比探究:(2)当![]() 时,把
时,把![]() 绕点
绕点![]() 逆时针旋转到如图3的位置时,请求出
逆时针旋转到如图3的位置时,请求出![]() 的值以及
的值以及![]() 与
与![]() 所在直线相交所成的锐角.
所在直线相交所成的锐角.
查看答案和解析>>
科目: 来源: 题型:
【题目】“禹州钧瓷”名扬天下,某网店专门销售某种品牌的钧瓷花瓶,成本为40元/件,每天销量![]() (件)与销售单价
(件)与销售单价![]() (元)之间存在一次函数关系,如图所示.
(元)之间存在一次函数关系,如图所示.
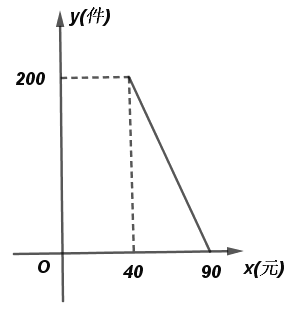
(1)求![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
(2)如果规定每天钧瓷花瓶的销售量不低于120件,当销售单价为多少元时,每天获取的利润最大,最大利润是多少元?
(3)该网店店主热心公益事业,决定从每天的销售利润中捐出100元给希望工程,为了保证捐款后每天剩余利润不低于2000元,试确定该钧瓷花瓶销售单价的范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,四边形ABCD是矩形,AD∥x轴,A(![]() ,
,![]() ),AB=1,AD=2.
),AB=1,AD=2.

(1)直接写出B、C、D三点的坐标;
(2)将矩形ABCD向右平移m个单位,使点A、C恰好同时落在反比例函数![]() (
(![]() )的图象上,得矩形A′B′C′D′.求矩形ABCD的平移距离m和反比例函数的解析式.
)的图象上,得矩形A′B′C′D′.求矩形ABCD的平移距离m和反比例函数的解析式.
查看答案和解析>>
科目: 来源: 题型:
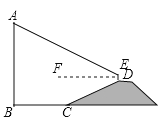
【题目】如图,![]() 是垂直于水平面的建筑物,为测量
是垂直于水平面的建筑物,为测量![]() 的高度,小红从建筑物底端
的高度,小红从建筑物底端![]() 出发,沿水平方向行走了52米到达点
出发,沿水平方向行走了52米到达点![]() ,然后沿斜坡
,然后沿斜坡![]() 前进,到达坡顶
前进,到达坡顶![]() 点处,
点处,![]() .在点
.在点![]() 处放置测角仪,测角仪支架
处放置测角仪,测角仪支架![]() 高度为0.8米,在
高度为0.8米,在![]() 点处测得建筑物顶端
点处测得建筑物顶端![]() 点的仰角
点的仰角![]() 为
为![]() (点
(点![]() ,
,![]() ,
,![]() ,
,![]() 在同一平面内),斜坡
在同一平面内),斜坡![]() 的坡度(或坡比)
的坡度(或坡比)![]() ,求建筑物
,求建筑物![]() 的高度.(精确到个位)(参考数据:
的高度.(精确到个位)(参考数据:![]() )
)
查看答案和解析>>
科目: 来源: 题型:
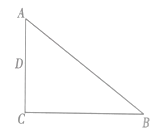
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 为
为![]() 边的中点.
边的中点.
(1)尺规作图:作出以![]() 为直径的圆
为直径的圆![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() .(保留作图痕迹,不写作法)
.(保留作图痕迹,不写作法)
(2)求证:![]() 是圆
是圆![]() 的切线.
的切线.
(3)当![]() 时,四边形
时,四边形![]() 是平行四边形,此时,四边形
是平行四边形,此时,四边形![]() 的形状为 .
的形状为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com