
科目: 来源: 题型:
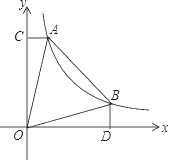
【题目】如图,A、B两点在反比例函数![]() (k>0,x>0)的图象上,AC⊥y轴于点C,BD⊥x轴于点D,点A的横坐标为a,点B的横坐标为b,且a<b.
(k>0,x>0)的图象上,AC⊥y轴于点C,BD⊥x轴于点D,点A的横坐标为a,点B的横坐标为b,且a<b.
(1)若△AOC的面积为4,求k值;
(2)若a=1,b=k,当AO=AB时,试说明△AOB是等边三角形;
(3)若OA=OB,证明:OC=OD.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,某大楼的顶部竖有一块宣传牌![]() .小明在山坡的坡脚
.小明在山坡的坡脚![]() 处测得宣传牌底部
处测得宣传牌底部![]() 的仰角为
的仰角为![]() ,沿山坡向上走到
,沿山坡向上走到![]() 处测得宣传牌顶部
处测得宣传牌顶部![]() 的仰角为
的仰角为![]() .已知山坡
.已知山坡![]() 的坡度
的坡度![]() ,
,![]() 米,
米,![]() 米.
米.
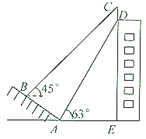
(1)求点![]() 距地面的高度;
距地面的高度;
(2)求大楼![]() 的高度.(测角器的高度忽略不计,结果精确到0.1米.参考数据:
的高度.(测角器的高度忽略不计,结果精确到0.1米.参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】某校为了解九年级男生1000米长跑的成绩,从中随机抽取了50名男生进行测试,根据测试评分标准,将他们的得分进行统计后分为A、B、C、D四等,并绘制成下面的频数分布表和扇形统计图
等级 | 成绩(得分) | 频数(人数) | 频率 |
A | 9~10分 | x | m |
B | 8~7 | 23 | 0.46 |
C | 6~5 | y | n |
D | 5分以下 | 3 | 0.06 |
(1)试直接写出x,y,m,n的值;
(2)求表示得分为C等的扇形的圆心角的度数;
(3)如果该校九年级共有男生400名,试估计这400名男生中成绩达到A等和B等的人数共有多少人?

查看答案和解析>>
科目: 来源: 题型:
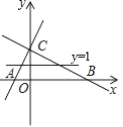
【题目】如图,直线y1=2x+2交x轴、y轴于点A、C,直线![]() 交x轴、y轴于点B、C,点P(m,1)是△ABC内部(包括边上)的一点,则m的最大值与最小值之差为( )
交x轴、y轴于点B、C,点P(m,1)是△ABC内部(包括边上)的一点,则m的最大值与最小值之差为( )
A.2B.2.5C.3D.3.5
查看答案和解析>>
科目: 来源: 题型:
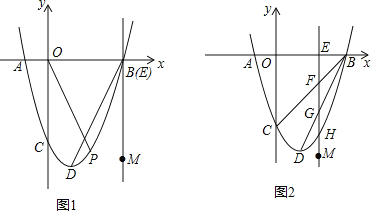
【题目】在平面直角坐标系中,已知抛物线y=![]() x2+bx+c的图象与x轴交于点A(﹣2,0),点B(6,0),与y轴交于点C,顶点为D.
x2+bx+c的图象与x轴交于点A(﹣2,0),点B(6,0),与y轴交于点C,顶点为D.
(1)求抛物线的解析式;
(2)点E是线段AB上的点,直线EM⊥x轴,设点E的横坐标为t.
①当t=6时(如图1),点P为x轴下方抛物线上的一点,若∠COP=∠DBM,求此时点P的横坐标;
②当2<t<6时(如图2),直线EM与线段BC,BD和抛物线分别相交于点F,G,H,试证明线段EF,FG,GH总能组成等腰三角形,如果此等腰三角形底角的余弦值为![]() ,求此等腰三角形的面积.
,求此等腰三角形的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】某学校准备购买若干台![]() 型电脑和
型电脑和![]() 型打印机.如果购买1台
型打印机.如果购买1台![]() 型电脑,2台
型电脑,2台![]() 型打印机,一共需要花费6200元;如果购买2台
型打印机,一共需要花费6200元;如果购买2台![]() 型电脑,1台
型电脑,1台![]() 型打印机,一共需要花费7900元.
型打印机,一共需要花费7900元.
(1)求每台![]() 型电脑和每台
型电脑和每台![]() 型打印机的价格分别是多少元?
型打印机的价格分别是多少元?
(2)如果学校购买![]() 型电脑和
型电脑和![]() 型打印机的预算费用不超过20000元,并且购买
型打印机的预算费用不超过20000元,并且购买![]() 型打印机的台数要比购买
型打印机的台数要比购买![]() 型电脑的台数多1台,那么该学校至多能购买多少台
型电脑的台数多1台,那么该学校至多能购买多少台![]() 型打印机?
型打印机?
查看答案和解析>>
科目: 来源: 题型:
【题目】直线l1,l2,l3,l4是同一平面内的一组平行线.
(1)如图1,正方形ABCD的4个顶点都在这些平行线上,若四条直线中相邻两条之间的距离都是1,其中点A,点C分别在直线l1和l4上,求正方形的面积.
(2)如图2,正方形ABCD的4个顶点分别在四条平行线上,若四条直线中相邻两条之间的距离依次为h1,h2,h3.
①求证:h1=h3.
②设正方形ABCD的面积为S,求证:S=2h12+2h1h2+h22.
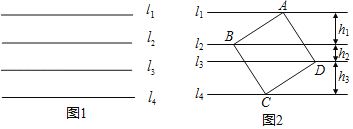
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com